sem resoluções.
|
Enunciado 2 Mudança de pneu |
Outros
Exercícios, s/d Anónimo |
sem resoluções.
|
Enunciado 3 Carro a trabalhar |
Outros
Exercícios, s/d Anónimo |
sem resoluções.
|
Enunciado 4 Olá a todos |
Outros
Exercícios, 1996 Miguel A. Brito |
| Resoluções: 1. Olatodos.c 2. Olatodos.bas 3. Olatodos.pas 4. Olatodos.for |
|
Enunciado 5 Operações sobre dois números |
Números
Exercícios, 1996 Miguel A. Brito |
| Resoluções: 1. Soma2.bas 2. Soma2.pas 3. Soma2.for 4. Soma2n.htm |
|
Enunciado 6 Classificação de um triângulo |
Geometria
, 1997 Pedro Pimenta |
| Resoluções: 1. Tri0.bas 2. Tri0.pas 3. Tri1.bas 4. Tri2.bas 5. Triang0.bas 6. Triang1.bas 7. Clatri.c 8. clatri.xls 9. Clatri.83p |
|
Enunciado 7 Olá ao utilizador |
Outros
Exercícios, 1996 Miguel A. Brito |
| Resoluções: 1. Olauser.bas 2. Olauser.pas |
|
Enunciado 8 Conversão de unidades |
Números
Exercícios, 1996 Miguel A. Brito |
sem resoluções.
|
Enunciado 9 Simulação do lançamento de uma moeda |
Simulação
Exercícios, 1996 Miguel A. Brito |
| Resoluções: 1. Moeda.83p |
|
Enunciado 10 Conversão de unidades |
Números
Exercícios, 1996 Miguel A. Brito |
sem resoluções.
|
Enunciado 11 Conversão de unidades |
Números
Exercícios, 1996 Miguel A. Brito |
| Resoluções: 1. Convcf2.83p |
|
Enunciado 12 Tabela de função |
Números
Ficha de problemas, 2001 Dias, M., Martins, F. |
Tabele a seguinte função
K(T) = K0/(T-T0)
entre T=200K e T = 700K em intervalos DT=50K, para os seguintes materiais:
| Sílica | K0 = 350 W/cm T0=68K |
| Material 1 | K0 = 400 W/cm T0=50K |
| Material 2 | K0 = 300 W/cm T0=70K |
sem resoluções.
|
Enunciado 13 Tabela de função |
Números
Ficha de problemas, 2001 Dias, M., Martins, F. |
Tabelar valores de ângulos em graus desde q = 0º a q = 360º com intervalos de Dq = 30º e os respectivos valores em radianos; tabelar as respectivas funções seno e cosseno.
sem resoluções.
|
Enunciado 14 Tabela de função |
Números
Ficha de problemas, 2001 Dias, M., Martins, F. |
Tabelar a função y(x) dada por (x2 + y2) = a2 (x2 + y2) ou, em coordenadas polares, r2 = a2 cos(2q).
Tome a=2 e tabele a função para 50 pares de valores x e y. Represente gráficamente y(x) e r(q).
sem resoluções.
|
Enunciado 15 Tabela de função |
Números
Ficha de problemas, 2001 Dias, M., Martins, F. |
Tabelar e representar graficamente as seguintes funções
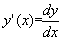
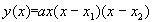
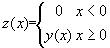
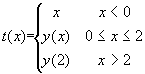
As funções devem ser tabeladas entre os valores xinicial e xfinal para nintervalos a fornecer pelo utilizador. Exemplo: a=0.5; x1=-1; x2=1.5; xinicial=-2; xfinal=3; nintervalos=20.
sem resoluções.
|
Enunciado 16 Tabela de funções |
Números
Ficha de problemas, 2001 Dias, M., Martins, F. |
sem resoluções.
|
Enunciado 17 Conversão de unidades |
Números
Introdução à Informática (2ª Edição), pág. 255, 1997 Rocha, N. P., Ramos, F. M., Oliveira, J. L. |
Elabore um Algoritmo para converter uma temperatura em graus centígrados para o correspondente em graus Fahrenheit (Fahrenheit= GCentígrados * 1.8 + 32).
| Resoluções: 1. Convcf2.83p |
|
Enunciado 18 Tabela de funções |
Números
Ficha de problemas, 2001 Dias, M., Martins, F. |
| Resoluções: 1. Convcf2.83p |
|
Enunciado 19 Operações aritméticas - I |
Números
Introdução à Informática (2ª Edição), pág. 255, 1997 Rocha, N. P., Ramos, F. M., Oliveira, J. L. |
Escreva um programa que leia dois números inteiros e que escreva o resultado da sua soma e do seu produto
sem resoluções.
|
Enunciado 20 Sequência de números |
Números
Ficha de problemas, 2001 Dias, M., Martins, F. |
- Ler um número inteiro positivo diferente de treze: dividir por dois se for par; multiplicar por três e somar um se for ímpar.
- Repetir o processo, imprimindo os valores resultantes, até o resultado ser igual a um.
- O número treze é considerado um número azarento, de modo que sempre que este valor surgir nos cálculos o programa deve avisar e o processo deve ser parado.
sem resoluções.
|
Enunciado 21 Operações aritméticas - II |
Números
Introdução à Informática (2ª Edição), pág. 255, 1997 Rocha, N. P., Ramos, F. M., Oliveira, J. L. |
Modifique o programa anterior de forma a apresentar igugalmente os resultados das seguintes operações
- Divisão real (primeiro/segundo)
- Subtracção (primeiro-segundo)
- Negação (-primeiro)
- Divisão inteira (primeiro DIV segundo)
- Resto da Divisão Inteira (primeiro MOD segundo)
sem resoluções.
|
Enunciado 22 Conversão de unidades |
Números
Ciência dos Computadores - Uma abordagem algorítmica, 1983 Tremblay, Bunt |
- Ler uma temperatura dada na escala Celsius e imprimir a equivalente em Fahrenheit (Fórmula de conversão: ºF = 32 + 1.8 ºC)
- Ler uma quantidade de chuva dada em polegadas e imprimir a equivalente em milímetros (25,4 mm = 1 polegada)
| Resoluções: 1. Convcf2.83p |
|
Enunciado 23 Área e volume de sólidos |
Geometria
Ficha de problemas, 2001 Dias, M., Martins, F. |
sem resoluções.
|
Enunciado 24 Nomes de pessoas |
Strings
Ciência dos Computadores - Uma abordagem algorítmica, 1983 Tremblay, Bunt |
Entrada: 'MONALISA', 'ALMEIDA PRADO'
Saída: ALMEIDA PRADO, MONALISA
| Resoluções: 1. Nomesob1.c |
|
Enunciado 25 Área de um quadrado |
Geometria
Introdução à Informática (2ª Edição), pág. 255, 1997 Rocha, N. P., Ramos, F. M., Oliveira, J. L. |
Escreva um programa que determine a área de um quadrado, fornecido o lado.
| Resoluções: 1. Areaq.c 2. aumquad.xls |
|
Enunciado 26 Triângulo rectângulo |
Geometria
Exercícios, 1996 Miguel A. Brito |
| Resoluções: 1. trirect.xls |
|
Enunciado 27 Lançamento de um dado |
Jogos
Exercícios, 1996 Miguel A. Brito |
| Resoluções: 1. Dados0.c 2. umdado.xls |
|
Enunciado 28 Área de um polígono |
Geometria
Colectânea do NDIG, 1996 Colectânea do NDIG |
sem resoluções.
|
Enunciado 29 Área de um pentágono |
Geometria
Pedro Pimenta, 2001 Pedro Pimenta |
| Escreva um programa que calcule a área de um pentágono regular, dado o raio da circunferência que o inscreve. | 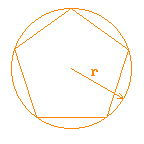 |
| Resoluções: 1. Apent.bas 2. Apent.c 3. Apent.for 4. Apent.xls |
|
Enunciado 30 Área de uma poligonal |
Geometria
Colectânea Prof. Barreiros Martins, 1994 Prof. Barreiros Martins |
| Resoluções: 1. Polig.cat |
|
Enunciado 31 Conversão de bases |
Números
Colectânea Prof. Barreiros Martins, 1994 Prof. Barreiros Martins |
sem resoluções.
|
Enunciado 32 Bases de numeração |
Números
Fundamental da Programação em 'C', pág. 43, 1998 Sampaio, I. e Sampaio, A. |
Escreva um programa que permita visualizar a representação hexadecimal dos seguintes valores em decimal: 0, 10, 15, 16, 29, 30.
sem resoluções.
|
Enunciado 33 Unidades |
Números
Colectânea do NDIG, 1996 Colectânea do NDIG |
sem resoluções.
|
Enunciado 34 Unidades de tempo |
Números
Ficha de problemas, 2001 Dias, M., Martins, F. |
| Tempo | = | 72627 | segundos | ||||
| = | 20 | horas | 10 | minutos | 27 | segundos |
sem resoluções.
|
Enunciado 35 Unidades |
Números
Fundamental da Programação em 'C', pág. 43, 1998 Sampaio, I. e Sampaio, A. |
Desenvolver um programa que escreva as horas, minutos e segundos correspondentes a um tempo dado em segundos.
sem resoluções.
|
Enunciado 36 Unidades |
Números
Fundamental da Programação em 'C', pág. 43, 1998 Sampaio, I. e Sampaio, A. |
Altere o programa anterior para que no final efectue a operação inversa.
sem resoluções.
|
Enunciado 37 Cálculo de p pelo método de Monte Carlo |
Geometria
Colectânea do NDIG, 1996 Colectânea do NDIG |
A figura ao lado mostra um quadrante de um círculo centrado no ponto (0,0) e de raio unitário, sendo também indicado um quadrado de lado unitário. A área do quadrado é de 1. A área do quadrante do círculo representado é de p/4. | 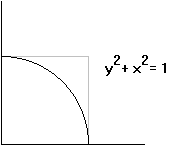 |
| Resoluções: 1. piest.bas 2. piest0.bas 3. piest1.bas |
|
Enunciado 38 Raízes de Equação quadrática |
Números
Ciência dos Computadores - Uma abordagem algorítmica, pág. 63., 1983 Tremblay, Bunt |
As raízes de uma equação quadrática da forma
ax2 + bx + c = 0
sem resoluções.
|
Enunciado 39 Preço de um carro |
Números
Ciência dos Computadores - Uma abordagem algorítmica, pág. 63., 1983 Tremblay, Bunt |
| Resoluções: 1. Precc1.ppt 2. Preccar.83p |
|
Enunciado 40 Prémio do seguro automóvel |
Números
Introdução à Informática (2ª Edição), pág. 258, 1997 Rocha, N. P., Ramos, F. M., Oliveira, J. L. |
Escreva um programa que calcule o valor do prémio de um seguro automóvel em função dos seguintes parâmetros de entrada:
- Preço Base de qualquer viatura = 10 000$00
- Idade da viatura:
até 5 anos = 5 000$00
entre 6 e 10 anos = 8 000$00
mais do que 10 anos = 10 000$00 + 500$00 por cada ano para além de 10. - Idade do condutor:
até 25 anos ou mais do que 60 anos = 5 000$00 - Agravamento por cada acidente = 2 000$00
| Resoluções: 1. Segauto.c 2. Segauto.xls 3. Segauto.m |
|
Enunciado 41 Par ou ímpar |
Números
Ciência dos Computadores - Uma abordagem algorítmica, pág. 85., 1983 Tremblay, Bunt |
(Este enunciado tb aparece em Rocha, N. P., Ramos, F. M., Oliveira, J. L., 1997, "Introdução à Informática" (2ª Edição), pág. 256)
| Resoluções: 1. Pnp.c 2. Pouimp.xls 3. Parimpar.for 4. Parimpar.m 5. Parimpar.83p |
|
Enunciado 42 Totobola |
Jogos
----, S/D S/A |
Faça um programa que gere aleatóriamente um chave simples para totobola.
| Resoluções: 1. totobola.m |
|
Enunciado 43 Determinar a eq. de uma recta dados dois pontos |
Geometria
Colectânea Prof. Barreiros Martins, 1994 Prof. Barreiros Martins |
sem resoluções.
|
Enunciado 44 Determinar a eq. de uma recta dados um ponto e um angulo. |
Geometria
Colectânea Prf. Barreiros Martins, 1994 Prof. Barreiros Martins |
sem resoluções.
|
Enunciado 45 Cálculo do consumo médio de um automóvel |
Números
Exercícios, 1994 Miguel Brito |
| Resoluções: 1. consaut.xls 2. consumaut.xls |
|
Enunciado 46 Contagem de números |
Números
Introdução à Informática (2ª Edição), pág. 237, 1997 Rocha, N. P., Ramos, F. M., Oliveira, J. L. |
Determinar o número de ocorrências de um dado número inteiro numa sequência de números terminada por 0.
| Resoluções: 1. contnums.xls |
|
Enunciado 47 Conversão de coordenadas polares para cartesianas |
Geometria
Exercícios, 1994 Miguel Brito |
y=rsen(q)). Codifique em 'C'.
sem resoluções.
|
Enunciado 48 Determinação do maior de 2 números |
Números
Exercícios, 1994 Miguel Brito |
| Resoluções: 1. Maiorde2.c 2. Maiorde2.xls |
|
Enunciado 49 Maior de dois |
Números
Introdução à Informática (2ª Edição), pág. 256, 1997 Rocha, N. P., Ramos, F. M., Oliveira, J. L. |
Escreva um programa que determine qual o maior de dois números introduzidos pelo operador.
sem resoluções.
|
Enunciado 50 Determinar a eq. de uma recta dados dois pontos |
Geometria
Colectânea Prof. Barreiros Martins, 1994 Prof. Barreiros Martins |
sem resoluções.
|
Enunciado 51 Determinar a posição relativa de um ponto em relação a uma recta |
Geometria
Colectânea Prof. Barreiros Martins, 1994 Prof. Barreiros Martins |
Programar a verificação se um dado ponto P(x,y) está ou não sobre a recta definida nos três problemas anteriores. E se está dentro do segmento definido pelos pontos P1 e P2 ou fora dele, do lado de cima ou do lado de baixo, e se o ponto está fora da recta se está para cima ou para baixo dela.
| Resoluções: 1. Ptorct.cat |
|
Enunciado 52 Determinar a intercepção de duas rectas |
Geometria
Colectânea Prof. Barreiros Martins, 1994 Prof. Barreiros Martins |
sem resoluções.
|
Enunciado 53 Traçado de troços de rectas e de poligonal |
Geometria
Colectânea Prof. Barreiros Martins, 1994 Prof. Barreiros Martins |
sem resoluções.
|
Enunciado 54 Conversão de horas e minutos em minutos |
Números
Exercícios, 1994 Miguel Brito |
sem resoluções.
|
Enunciado 55 Determinação do maior de 3 números |
Números
Exercícios, 1994 Miguel Brito |
| Resoluções: 1. Md3.xls 2. Md3.mws 3. Md3.m 4. Md3.htm 5. Md3.c |
|
Enunciado 56 Menor de 3 |
Números
Introdução à Informática (2ª Edição), pág. 256, 1997 Rocha, N. P., Ramos, F. M., Oliveira, J. L. |
Escreva um programa que determine o menor de três números indicados pelo utilizador.
sem resoluções.
|
Enunciado 57 Apresentação ordenada de 3 números |
Números
Exercícios, 1994 Miguel Brito |
sem resoluções.
|
Enunciado 58 Operações com 2 números |
Números
Exercícios, 1994 Miguel Brito |
Elabore um Algoritmo que peça dois números ao utilizador, e apresente o resultado da sua divisão (não se esqueça de verificar os casos de indeterminação, e divisão por zero). Codifique em 'C'.
sem resoluções.
|
Enunciado 59 3 bolas de totoloto |
Jogos
Exercícios, 1994 Miguel Brito |
| Resoluções: 1. Tbolas.83p |
|
Enunciado 60 Latas de tinta para pintar um tanque |
Números
BASIC Ilustrado, 1977 Donald Alcock |
|
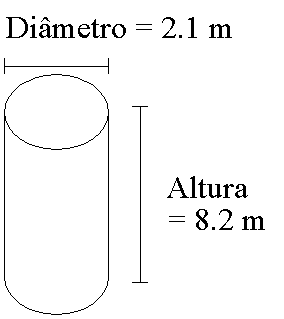 |
| Resoluções: 1. Latasr.bas |
|
Enunciado 61 Limites |
Geometria
Colectânea do NDIG, 1996 Colectânea do NDIG |
| Construa um programa que dado o par de números reais (x,y), averigue se o ponto por ele representado é interior ao triângulo delimitado pelas três rectas indicadas: | 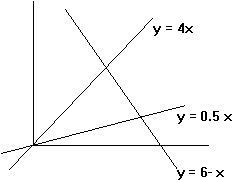 |
sem resoluções.
|
Enunciado 62 Traçado de um triângulo |
Geometria
Colectânea Prof. Barreiros Martins, 1994 Prof. Barreiros Martins |
- ou pelos seus três lados
- ou por dois lados e o ângulo correspondente
- ou por um lado e os dois ângulos adjacentes
sem resoluções.
|
Enunciado 63 Área de um triângulo |
Geometria
Colectânea Prof. Barreiros Martins, 1994 Prof. Barreiros Martins |
sem resoluções.
|
Enunciado 64 Área de um triângulo |
Geometria
Ciência dos Computadores - Uma Abordagem Algorítmica, pág. 63, 1981 Tremblay & Bunt |
área = SQRT (T*(T-S1)*(T-S2) * (T-S3))
sem resoluções.
|
Enunciado 65 Conversão de unidades |
Números
Ciência dos Computadores - Uma Abordagem Algorítmica, pág. 69, 1981 Tremblay & Bunt |
- Converter resultados de salto em altura, relatados em metros, para pés e polegadas (ft e in) (1 pé vale 12 polegadas e metro vale 39,37 polegadas)
- Dado o tempo para uma corrida de 100 metros, calcular o seu tempo para 100 jardas. Supor que o atleta corra a uma velocidade constante (1 jarda vale 3 pés ou 0.9144 metros).
sem resoluções.
|
Enunciado 66 Conversão de unidades |
Números
Ciência dos Computadores - Uma Abordagem Algorítmica, pág. 69, 1981 Tremblay & Bunt |
100 Francos Franceses = | 21.55 Dólares Canadenses |
1 Dólar Americano = | 1.06 Dólares Canadenses |
100 Marcos Alemães = | 43.20 Dólares Canadenses |
1 Libra Inglesa = | 1.84 Dólares Canadenses |
100 Coroas Suecas = | 24.25 Dólares Canadenses |
100 Dracmas Gregos = | 2.95 Dólares Canadenses |
- Ler uma quantidade em francos franceses e imprimir o equivalente em dólares canadenses
- Ler uma quantidade em dólares americanos e imprimir o equivalente em ambos, coroas suecas e francos franceses
- Ler uma quantidade em dracmas gregos e imprimir o equivalente em libras inglesas
- Ler uma quantidade em dólares canadenses e imprimir o equivalente em ambos, dólares americanos e marcos alemães
sem resoluções.
|
Enunciado 67 Volume de uma esfera |
Geometria
Introdução à Informática (2ª Edição), pág. 255, 1997 Rocha, N. P., Ramos, F. M., Oliveira, J. L. |
Escreva um programa que determine o volume de uma esfera, fornecido o respectivo raio.
sem resoluções.
|
Enunciado 68 Função sin() |
Números
Ficha de problemas, 2001 Dias, M., Martins, F. |
Desenvolva duas rotinas VBA que permitam tabelar a função sin(x) entre 0 e 2 p com passo igual a p/6. Na primeira subrotina use um ciclo For ... Next e na segunda um ciclo Do...Loop
sem resoluções.
|
Enunciado 69 Volume de um tronco de cone |
Geometria
Colectânea Prof. Barreiros Martins, 1994 Prof. Barreiros Martins |
sem resoluções.
|
Enunciado 70 Área de segmento de círculo |
Geometria
Colectânea Prof. Barreiros Martins, 1994 Prof. Barreiros Martins |
sem resoluções.
|
Enunciado 71 Volume de segmento de esfera |
Geometria
Colectânea Prof. Barreiros Martins, 1994 Prof. Barreiros Martins |
Programar a área total de um tal segmento de esfera.
sem resoluções.
|
Enunciado 72 Intersecção de recta com círculo |
Geometria
Colectânea Prof. Barreiros Martins, 1994 Prof. Barreiros Martins |
sem resoluções.
|
Enunciado 73 Traçado de uma parábola |
Geometria
Colectânea Prof. Barreiros Martins, 1994 Prof. Barreiros Martins |
- ou pelas coordenadas de três dos seus pontos
- ou pelas coordenadas de dois dos seus pontos e abcissa do ponto de máximo (ou de mínimo)
- altere o programa para que passe a indicar também o mínimo valor lido
- altere o programa para que passe a indicar também o valor médio de todos os valores lidos.
- Na matemática, a expressão seguinte é sempre verdadeira:
| sin(x) | £ 1 Preparar um algoritmo a fim de verificar esta propriedade para a função embutida SIN para valores de x no intervalo -10.0 a +10.0 com passos de 0.2. - Na matemática, a seguinte propriedade é mantida:
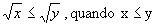
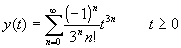
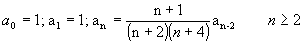
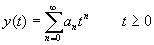
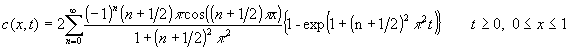
- 1% por cada ano de idade superior a 25 anos.
- 3% por cada ano de casa.
- 5% por cada filho ou outro dependente.
- Introduza o número usando uma InputBox;
- Se n não for inteiro, apresente uma mensagem de erro e reinicie a rotina;
- Divida n sucessivamente por todos os inteiros entre 2 e n / 2;
- Em cada divisão verifique se o resto da divisão inteira é nulo:
- Se o resto for nulo então o número não é primo; escrever a mensagem respectiva e sair;
- Se o resto não for nulo em nenhuma divisão então o número é primo; escrever a mensagem respectiva e voltar ao inicio.
- procure desenvolver algoritmos alternativos e classifique essas alternativas relativamente à velocidade de cálculo
- procure encontrar números amigos tão grandes quanto possível
- O mínimo, o máximo, e a média dos elementos do vector
- O número de vezes que ocorre cada elemento.
- Verifique se um dado valor pertence ao não ou vector dado
- Caso pertença, indique a(s) posição (ões) em que ocorre
Determine o máximo e o mínimo do vector, assim como a(s) posição (ões) em que ocorre(m) - Determine se uma dada sequênca de números (x, y) ocorre ou não no vector original, quantas vezes, e em que posição (ões)
- Determine se uma dada sequência (x, ?, y, z), em que ? pode ser uma valor qualquer, ocorre ou não no vector original, quantas vezes, e em que posição (ões)
- Utilizando a função random, dê palpites para chaves de totoloto.
- Altere o programa de forma a gerar S chaves e implemente as seguintes estatísticas:
- Quantas vezes saíu cada número ?
- Quais os números que saíram mais vezes ?
- Quais os números que saíram menos vezes ?
- O jogador começa a jogar, lançando quatro dados;
- Se o resultado for par, o jogador perde 10 pontos;
- Se o resultado for ímpar, o jogador ganha 10 pontos;
- Se o resultado for maior que 15, na próxima vez o jogador joga com três dados;
- Se o resultado for menor que 5, na próxima vez o jogador joga com quatro dados;
- Se ocorreram duas jogadas seguidas de resultado par, o jogador ganha 1 ponto;
- Se ocorreram duas jogadas seguidas de resultado ímpar, o jogador perde um ponto.
- O trajecto mais económico entre duas quaisquer cidades (X e Y);
- O trajecto mais económico entre duas quaisquer cidades (X e Y) passando por uma outra (Z);
- O trajecto mais económico entre duas quaisquer cidades (X e Y) não passando por outra (Z);
- O trajecto menos económico entre duas quaisquer (X e Y) e que passa uma e uma só vez por cada uma das outras cidades.
- Encontre dois números primos consecutivos cuja diferença seja superior a cem.
- Encontre dois números primos consecutivos cuja diferença seja superior a mil.
- A quilometragem obtida por litro de gasolina entre cada par de paradas de reabastecimento;
- A quilometragem obtida por litro de gasolina em toda a viagem.
- Inicie o preenchimento do quadrado pela casa imediatamente abaixo do elemento central, colocando o nº 1;
- O elemento seguinte será colocado na posição 'um quadrado mais abaixo' e 'um quadrado mais à direita' - desde que esse lugar não esteja já ocupado;
- Se, ao seguir a regra 'abaixo-direita', 'sairmos' do espaço da matriz, devemos imaginar que após a última coluna da matriz encontramos de novo a primeira coluna, e após a última linha encontramos de novo a primeira linha da matriz;
- Se, seguindo a regra 'abaixo-direita', chegarmos a uma casa já ocupada, seguimos a regra 'abaixo-esquerda';
- O preenchimento da matriz termina quando tivermos distribuído os N2 números pelos N2 elementos da matriz de lado N.
- Série geométrica: S = 1 + 1/2 + 1/4 + 1/8 + 1/16 + ... , com um número N de termos, dado pelo utilizador;
- Série geométrica: S = 1 + 1/2 + 1/4 + 1/8 + 1/16 + ... , calculada até que o termo seja inferior a um dado valor e, dado pelo utilizador;
- Série harmónica: S = 1 + 1/2 + 1/3 + 1/4 + 1/5 + ... , calculada com um número N de termos, dado pelo utilizador;
- Série harmónica alternada: S = 1 - 1/2 + 1/3 - 1/4 + 1/5 - ... , calculada com um número N de termos, dado pelo utilizador;
- Cálculo de p: p = 4 ´( 1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + ...) , calculada com um número N de termos, dado pelo utilizador;
- Aceite a caracterização de várias pessoa através dos seguintes items;
Nome Idade Sexo Interesses (Desporto, arte, música, dança, fotografia, gastronomia, TV, ...)
- Ordene e liste as pessoas por ordem alfabética de Nome, ou ordem numérica de idade;
- Permita modificar a caracterização de uma pessoa, ou eliminá-la da lista.
- Atribua "índices de (in)compatibilidade" entre pessoas, com base nos items atrás indicados, e deverá apresentar uma lista das pessoas "mais" e "menos" compativeís. (O programa deverá indicar quanto tempo foi necessário para o cálculo dos índices de (in)compatibilidade).
- Guarde em ficheiro a caracterização das pessoas, de modo a poder aumentar o nº de "fichas" entre corridas do mesmo programa.
- O peso médio e a idade média para cada um dos quarenta times.
- O peso médio e a idade média de todos os participantes da Taça de Ouro
- Calcule o número mínimo de notas/moedas a dar de troco, na compra de um produto de valor Y, pago com uma nota de valor X.
- Supondo que, no início, o "computador" possui um determinado número de notas/moedas, o programa deverá indicar, após execução (um número variável de "compras"):
- Seja capaz de gerar N cartões de bingo diferentes;
Os cartões de bingo são compostos por quinze números, obedendo à seguinte regra: 5 dos números devem pertencer ao intervalo 1-29, outros cinco ao intervalo 30-59 e os restantes 5 ao intervalo 60-90.
- Simule a participação de M jogadores, cada um com Xm cartões (O número de jogadores deverá ser menor que o número de cartões, e dois jogadores diferentes não poderão ter cartões iguais).
- Proceda à simulação do jogo do bingo, sorteando números na gama 1-100, até identificar o cartão vencedor. O programa deverá indicar o tempo necessário à condução da partida.
- Passou em todos os exames
- Passou em A, B e D, mas não em C ou E
- Passou em A e B, C ou D, mas não em E
- Percentagem de motoristas com menos de 25 anos
- Percentagem de mulheres
- Percentagem de motoristas maiores de 18 anos, mas menores de 25 anos
- Percentagem de motoristas com registo feito fora de São Paulo
- Preparar um algoritmo para calcular e tabular os valores da função
f(x,y) = (x2-y2)/(x2+y2)
parax=2,4,6,7 e
y=6,9,12,15,18,21 - Preparar um algoritmo para calcular o número de pontos como coordenadas de valor inteiro contidas na elipse:
x2/16 + y2/25 = 1
Nota:- Os pontos no interior da curva acima são considerados dentro da elipse
- Os valores das coordenadas estão limitados pelos eixos maior e menor da elipse (isto é, -4 <= x <= 4 e -5 <= y <= 5)
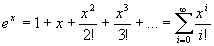
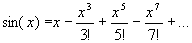
- Dado um valor para n0, gerar a sequência respectiva (p. ex.: , n0 = 7 { 7, 22, 11, 34, ...});
- A sucessão poderá atingir um ciclo do tipo 1, 4, 2, 1, 4, 2, ...
O programa deverá testar se uma situação deste tipo foi atingida e, em caso afirmativo, determinar o tempo e nº de iterações necessárias a atingir essa situação.
- Para cada sequência, o programa deverá indicar:
- o nº de números primos que foram encontrados até atingir o ciclo respectivo.
- o tempo médio de cada iteração
- o nº de números primos que foram encontrados até atingir o ciclo respectivo.
- Preparar um algoritmo para calcular o valor da economia que você teria no final de 10 anos se você depositasse Cr$ 100 000.00 cada mês. Assumir uma constante anual de razão de juros de 6% composta a cada 6 meses (Isto é, juros no valor de 3% são adicionados a cada 6 meses).
- Desejamos investir uma soma de dinheiro que crescerá a X cruzeiros em Y anos. Se a taxa de juros é R por cento, então o valor que devemos investir (valor atual de X) é dado pela fórmula
X/(1+.01R)y
Preparar um algoritmo que imprima uma tabela dos valores atuais de Cr$ 5 000 000.00 à taxa de juro de 7,5%, para períodos de 1 a 21 anos, de 2 em 2 anos. - Todas as mulheres loiras, olhos azuis, altura entre 160 e 175 cm, pesando menos de 60 kg
- Todos os homens de olhos castanhos, altura maior do que 175, pesando entre 75 kg e 95 kg
- O utilizador indicará o nº de lances a efectuar;
- Durante a simulação, o programa deverá, pelo menos, visualizar:
- as sequências contíguas ascendentes obtidas (e. g. 1-2-3, 5-6-7)
- os lances em que um dos números seja à soma dos outros dois
- os lances em que todos os números sejam ímpares
- a ocorrência de dois lances repetidos (e. g. 6-8-1 seguido de 6-8-1)
- No final da simulação, o programa deverá indicar o seguinte:
- o tempo de execução do programa;
- percentagem de sequências contíguas ascendentes obtidas (e. g. 1-2-3, 5-6-7)
- percentagem de lances em que um dos números é igual à soma dos outros dois
- percentagem de lances em que todos os números são ímpares
- Inicialize a matriz com valores aleatórios entre 1 e 100;
- Identifique qual o maior elemento da matriz, e indique a sua posição (apenas uma mesmo que haja vários valores iguais);
- Efectue as trocas de linhas e colunas necessárias por forma a que aquele elemento ocupe o centro da matriz.
- Inicialize a matriz com valores aleatórios entre 2 e 9, com excepção da última linha e da última coluna;
- Preencha as últimas linha e coluna, sabendo que os seus elementos resultam da soma dos restante elementos da mesma coluna ou da mesma linha, respectivamente;
- O último elemento da matriz resulta da soma dos elementos da diagonal principal.
- Em que jornada se verificou um número maior de espectadores;
- Para que estádio, ao longo do ano, a percentagem de polícias, em relação ao numero total de espectadores, foi superior;
- Em que jogos não estiveram crianças.
- Em cada lance, um jogador tenta adivinhar o naipe de uma carta escondida, num máximo de três tentatives, sendo pontuado da seguinte forma:
- 4 pontos se acertar à primeira tentativa;
- 2 pontos se acertar à segunda tentativa;
- 1 ponto se acertar à terceira tentativa.
- Poderá estar envolvido um número variável de jogadores (num mínimo de 2);
- Após o lance de um jogador, o computador decidirá aleatóriamente qual o próximo jogador, atribuindo-lhe uma probabilidade inversamente proporcional à sua pontuação (Se o jogador 1 tem 10 pontos e o jogador 2 tem 20, o jogador 1 terá uma probabbilidade duas vezes maior que o jogador 2 de continuar a jogar).
- No final do jogo (quando um dos jogadores atingir 50 pontos), o programa deverá indicar:
- qual a média de pontos por lance, no conjunto de todos os jogadores.
- quantos lances efectuou cada jogador e quantos pontos obteve em cada lance
- qual o jogador com melhor média de pontos por lance
- qual o jogador com pior média de pontos por lance.
- Procurar registo dado o nome
- Procurar registo dado o nº telefónico
- Introduzir um novo registo
- Apagar um registo
- Listar todos os registos
- Apagar toda a lista
- uma string que contém uma pergunta ou resposta,
- um valor que aponta para a pergunta seguinte a fazer no caso da resposta do utilizador ser afirmativa, e
- um valor que aponta para a pergunta seguinte a fazer no caso da resposta ser negativa.
- Desenvolva uma função para ler uma matriz com um máximo de MAXC colunas
- Escreva uma função que multiplique duas matrizes dadas como argumentos
- Elabore uma versão simplificada da função itoa, cujos parâmetros são o número a converter e a string que conterá o número convertido
- Escreva uma função que dada uma string (como argumento) a converta num inteiro.
- Escreva uma função que dada uma string como argumento a inverta.
- Quantos automóveis foram registados com menos de 100 000 km;
- Quantos automóveis foram registados com marca iniciada por 'A'ou 'P';
- A média da kilometragem dos automóveis de cor "preta"
- A média da kilometragem dos automóveis de marca iniciada por 'W' ou 'F'
- A marca do automóvelcom maior kilometragem (no case de empate, devolva o primeiro automóvel a ser encontrado)
- A marca do automóvelcom maior kilometragem (no case de empate, devolva o último automóvel a ser encontrado)
- Quantos livros foram registados com menos de 500 páginas;
- A posição, no vector, do(s) livro(s) mais antigo(s)
- Quantos livros foram registados com Autor iniciado por 'L'ou 'E';
- O nome do Autor com mais livros escritos (ooppsssss !!, esta é mais complicada !)
- O Autor do livro com o título mais longo (No caso de empate, sorteie um dos livros em causa) (ooppsssss !!, esta é mais complicada !)
- Quantos automóveis foram registados com menos de 100 000 km;
- A média da kilometragem dos automóveis de cor "preta";
- Quantos jogadores foram registados pertencentes a uma equipa com nome iniciado por 'A' ou 'B';
- Quais os jogadores com menos de 23 anos e que pertençam a uma equipa com o nome começado por 'P';
sem resoluções.
|
Enunciado 74 Traçado de uma parábola |
Geometria
Colectânea Prof. Barreiros Martins, 1994 Prof. Barreiros Martins |
Programar a intercepção da parábola y = ax2+bx+c com o eixo dos xx. Contemplar o caso de não haver intercepção e então verificar se a parábola fica para cima ou para baixo do eixo dos xx.
sem resoluções.
|
Enunciado 75 Movimento |
Números
Colectânea Prof. Barreiros Martins, 1994 Prof. Barreiros Martins |
Programar o cálculo da posição s=f(t) de um móvel que sobe um plano inclinado definido pela base b e altura h sujeito a uma força constante F paralela ao plano inclinado, que actua durante t1 segundos, tendo o móvel a massa m (movimento uniformemente acelerado). O móvel parte da base do plano inclinado com a velocidade inicial nula. Contemplar os casos de o móvel ultrapassar o cimo do plano inclinado; o de não chegar a atingir o cimo do mesmo plano e o de não arrancar da base.
sem resoluções.
|
Enunciado 76 Implemente a função potência |
Números
Exercícios, 1994 Miguel Brito |
sem resoluções.
|
Enunciado 77 Classificação de notas |
Números
Exercícios, 1994 Miguel Brito |
Elabore um Algoritmo que converta uma classificação de 1 a 5 (inteiros), em "mau", "medíocre", "suficiente", "bom" e "muito bom", respectivamente. Codifique em 'C'.
sem resoluções.
|
Enunciado 78 Contagem de números |
Números
Introdução à Informática (2ª Edição), pág. 239, 1997 Rocha, N. P., Ramos, F. M., Oliveira, J. L. |
Escrever no ecrã os números pares existentes entre dois números limite definidos pelo Operador, e indicar quantos números pares existem nessa gama de números.
| Resoluções: 1. Contpar2.c |
|
Enunciado 79 Máximo, mínimo e média |
Números
Introdução à Informática (2ª Edição), pág. 257, 1997 Rocha, N. P., Ramos, F. M., Oliveira, J. L. |
Escreva um programa que leia uma série de números até que seja digitado o número zero e que indique qual o maior número introduzido
| Resoluções: 1. Mmm.83p |
|
Enunciado 80 Somatório de 10 |
Números
Introdução à Informática (2ª Edição), pág. 257, 1997 Rocha, N. P., Ramos, F. M., Oliveira, J. L. |
Considere a entrada de uma série de 10 números e desenvolva um programa que apresente o somatório de todos os números e o somatório de todos os números negativos.
sem resoluções.
|
Enunciado 81 Sequência de números |
Números
Introdução à Informática (2ª Edição), pág. 241, 1997 Rocha, N. P., Ramos, F. M., Oliveira, J. L. |
Dado um valor inicial entre 10 e 20 e um incremento entre 5 e 10, escrever no ecrã os números entre o valor inicial e 1000 que se obtêm adicionando, sucessivamente a partir do valor inicial, o incremento ao valor anterior.
sem resoluções.
|
Enunciado 82 Palavras de uma frase |
Strings
Introdução à Informática (2ª Edição), pág. 245, 1997 Rocha, N. P., Ramos, F. M., Oliveira, J. L. |
Escrever no ecrã uma frase composta por palavras introduzidas pelo operador; o número de palavras da frase deve ser definido pelo operador.
sem resoluções.
|
Enunciado 83 Escrever uma frase no ecrã |
Strings
Introdução à Informática (2ª Edição), pág. 247, 1997 Rocha, N. P., Ramos, F. M., Oliveira, J. L. |
sem resoluções.
|
Enunciado 84 Tabela ASCII |
Strings
Introdução à Informática (2ª Edição), pág. 249, 1997 Rocha, N. P., Ramos, F. M., Oliveira, J. L. |
Escrever no ecrã os caracteres da tabela ASCII entre 33 e 126
sem resoluções.
|
Enunciado 85 Cálculo de salário |
Números
Ciência dos Computadores - Uma Abordagem Algorítmica, pág. 69, 1981 Tremblay & Bunt |
A Companhia de Carros Usados João Honesto paga a seus empregados um salário de Cr$ 60000.00 por mês mais uma comissão de Cr$ 5000.00 para cada carro vendido mais 5% do valor da venda. Todo mês a companhia prepara um cartão perfurado para cada vendedor contendo seu nome, o número de carros vendidos e o valor total das vendas. Prepare um algoritmo para calcular e imprimir o salário do vendedor num dado mês. Testar o algoritmo completamente, utilizando um conjunto apropriado de dados.
sem resoluções.
|
Enunciado 86 Energia de Coesão |
Números
Ciência dos Computadores - Uma Abordagem Algorítmica, pág. 70, 1981 Tremblay & Bunt |
Três massas, m1, m2 e m3 estão separadas por distâncias r12, r13, r23, como mostrado na figura. Se G é a constante de gravitação Universal, a energia de Coesão mantendo a massa das partículas é dada pela fórmula 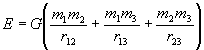 Prepare um algoritmo para ler valores de m1, m2, m3, r12, r13 e r23; calcular e imprimir a energia de coesão, imprimindo também os valores iniciais dados. Para a massa em kg e a distância em metros, G = 6.67 x 10-11 Nm2/kg2. Os valores de m1, m2, m3 são perfurados no primeiro cartão, os valores de r12, r13 e r23 são perfurados no segundo. Assumir que todos os dados são perfurados como valores reais. | 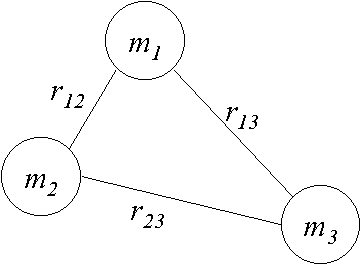 |
| Resoluções: 1. Ecoesao.c 2. Ecoes.m 3. Ecoes.htm 4. Ecoes.mws 5. Ecoes.xls |
|
Enunciado 87 Classificação de notas |
Números
Exercícios, 1994 Miguel Brito |
sem resoluções.
|
Enunciado 88 Calculadora com as 4 operações básicas |
Outros
Exercícios, 1994 Miguel Brito |
| Resoluções: 1. Quatroop.xls |
|
Enunciado 89 Soma dos quadrados dos 100 primeiros números |
Números
Ciência dos Computadores - Uma abordagem algorítmica, pág. 116., 1983 Tremblay, Bunt |
sem resoluções.
|
Enunciado 90 Propriedades matemáticas |
Ciência dos Computadores - Uma abordagem algorítmica, pág. 116., 1983 Tremblay, Bunt |
| Resoluções: 1. Pmata.m 2. Pmata.xls |
|
Enunciado 91 Temperatura três cidades |
Estatística
Exercícios, 1994 Miguel Brito |
Elabore um Algoritmo que dadas três temperaturas tiradas numa cidade ao longo do dia, indique qual a máxima e qual a mínima. Codifique em 'C'.
| Resoluções: 1. Maxt3c.c |
|
Enunciado 92 Salários de funcionários |
Números
Exercícios, 1994 Miguel Brito |
Numa empresa, os funcionários são pagos a 250$/hora. Pretende-se um algoritmo que a partir da leitura do número de horas de laboração de um empregado em cada um dos 5 dias da semana, e tendo em conta que os descontos de 15% para a segurança social e 10% de IRS, calcule os vencimentos bruto e líquido do funcionário, bem como os respectivos descontos. Codifique em 'C'.
sem resoluções.
|
Enunciado 93 Série |
Números
Ficha de problemas, 2001 Dias, M., Martins, F. |
Desenvolva uma subrotina em VBA para determinar a soma sucessiva dos termos da série até que o valor de um termo seja inferior em valor absoluto a 10-6. Escreva para uma folha Excel: o número do termo da série, o respectivo valor e o valor da soma.
sem resoluções.
|
Enunciado 94 Média de 4 valores |
Estatística
Exercícios, 1994 Miguel Brito |
Dada uma sequência de 4 números introduzidos pelo utilizador, elabore um Algoritmo que calcule a média dos valores positivos (ou nulos), ou seja, ignorando os valores negativos. Codifique em 'C'.
sem resoluções.
|
Enunciado 95 Cálculo do desvio padrão de cinco números |
Estatística
Ciência dos Computadores - Uma abordagem algorítmica, 1983 Tremblay, Bunt |
Preparar um algoritmo para calcular a estatística desvio padrão, s, de cinco números. A fórmula requerida é:
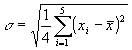
onde x1, x2, ..., x5 são cinco valores a serem lidos, 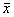 indica a média e
indica a média e  indica o somatório dos cinco termos indicados.
indica o somatório dos cinco termos indicados.
sem resoluções.
|
Enunciado 96 Tabela de funções |
Números
Ficha de problemas, 2001 Dias, M., Martins, F. |
Escreva subrotinas VBA para tabular as seguintes funções:
sem resoluções.
|
Enunciado 97 Tabela de funções |
Números
Ficha de problemas, s/d Anónimo |
Construa um programa que dado um valor de x real, calcule;
f(x) = 5, se x=2, (x+4)/(x-2) se x<>2
sem resoluções.
|
Enunciado 98 Tabela de funções |
Números
Ficha de problemas, s/d Anónimo |
Construa um programa que dados os valores de k e x, calcule; Tabelar a seguinte função com incremento h=0.05 Elabore um programa que tabele a função: Elabore um programa que tabele a função: Elabore um programa que permita construir uma pirâmide de números. Por exemplo, para n=4 tem-se: O cardápio de uma casa de hamburguer é dado abaixo. Preparar um algoritmo para ler a quantidade de cada item comprado e calcular a conta final. Construir um algoritmo que leia valores inteiros positivos até encontrar um negativo. Dar como resultado o valor máximo e mínimo entrados. Elabore um Algoritmo que dado um número, indique se ele é divisível por 3 ou não. Codifique em 'C'. Elabore um Algoritmo que dados dois números, indique se algum deles é múltiplo do outro. Codifique em 'C'. Elabore um Algoritmo que calcule o vencimento de um funcionário, sabendo que este é calculado adicionando a um dado vencimento base, as seguintes parcelas: Elabore um Algoritmo que pergunte o nome ao utilizador, e responda aleatoriamente «"Olá ", nome, "!"», «"Como está ", nome, "?"» ou «"Prazer em vê-lo ", nome, "!"». Codifique em 'C'. Seja a função f(x,i) dada pela equação apresentada a seguir e em que i é uma variável inteira e x é uma variável real. Desenvolva a programação de uma função em VBA que permita avaliar o valor de f(x,i). Construa um programa que determine todas as sequências possíveis utilizando as letras S, O, P e T. Construa um programa que verifique se uma dad string é, ou não, uma capicua. Construa um programa que transforme uma string do tipo: Elabore um algoritmo que dado um valor determinado valor em escudos, indique quantas moedas de 100$, 50$, 10$, 5$ e 1$, serão necessárias para perfazer essa quantia (com o mínimo de moedas possível). Codifique em 'C'. Elabore um algoritmo e escreva um programa que calcule o número mínimo de notas/moedas a dar de troco na compra de um produto de valor Y, pago com uma nota no valor de X. Elabore um Algoritmo que dada a nota de um aluno, entre 0.0 e 20.0, indique se está Aprovado (nota ³ 9.5), Reprovado (nota < 7.5), ou para Exame (7.5 ³ nota > 9.5); valide os casos fora de limites. Codifique em 'C'. Preparar um algoritmo para ler a base e a altura de um triângulo e imprimir a área deste triângulo (área = base * altura / 2). Durante a preparação dos dados para este algoritmo, é possível que se cometa um erro e entrem valores negativos para a base ou para a altura. Isto é indesejável, pois a área impressa será negativa. Prever no algoritmo a possibilidade de verificar valores negativos na entrada. Se um valor negativo é encontrado, imprimir uma mensagem de erro identificando este valor como base ou altura (isto permite corrigir o erro mais facilmente). Testar o algoritmo cuidadosamente. Tomar cuidado no caso de ambos os valores serem negativos. Isto produziria uma área positiva e o erro não seria detectado. Preparar um algoritmo para ler os comprimentos dos três lados de um triângulo (S1, S2 e S3) e determinar que tipo de triângulo temos, com base nos seguintes casos. Seja A o maior dos lados de S1, S2 e S3 e B e C os outros dois. Então: O Departamento do Meio Ambiente mantém três listas de indústrias conhecidas por serem altamente poluentes da atmosfera. Os resultados de várias medidas são combinados para formar o que é chamado de "índice de poluição". Isto é controlado regularmente. Normalmente os valores caem entre 0.05 e 0.25. Se o valor atingir 0.30, as indústrias da lista A serão chamadas a suspender as operações até que os valores retornem ao intervalo normal. Se o índice atingir 0.40, as indústrias da lista B serão notificadas também. Se o índice exceder 0.50, indústrias de todas as três listas serão avisadas para suspenderem as actividades. Preparar um algoritmo para ler o índice de poluição e indicar as notações apropriadas. Considere que as seguintes equações descrevem a evolução do nº de coelhos e raposas num determinado ecossistema, ano após ano:
f(x) =
exp(-abs(x+k), se (-2k-1) < x < -1
exp(-abs(x)), se -1 <= x <= 1
exp(-abs(x-k), se 1
Enunciado 99
Tabela de funções
Números
Ficha de problemas, s/d
Anónimo
f(x) = [(1+2x) ln(x)]/(x+3) com 1<=x<=2
sem resoluções.
Enunciado 100
Tabela de funções
Números
Ficha de problemas, s/d
Anónimo
f(x) = sum(n=1, 50) (nx+3)/(n+2x) * Prod(n=1,20) (5x+n)/(2n)
sem resoluções.
Enunciado 101
Tabela de funções
Números
Ficha de problemas, s/d
Anónimo
P(alfa, x) = sum(n=0, x) [exp(alfa)*alfa/n!] para alfa a variar entre 0.01 e 10 com incremento h=0.01 e x inteiro não negativo (x=0,1,2,...)
sem resoluções.
Enunciado 102
Pirâmide de números
Números
Ficha de problemas, s/d
Anónimo
1
121
12321
1234321
sem resoluções.
Enunciado 103
Cálculo de uma factura
Estatística
Ciência dos Computadores - Uma abordagem algorítmica, pág. 63, 1983
Tremblay, Bunt
Mona's Burguer Hamburguer (Cr$ 650) p Cheeseburguer (Cr$ 750) p Batatas fritas (Cr$ 350) p Refrigerantes (Cr$ 30) p Milkshake (Cr$ 50) p Total __________ Resoluções:
1. Monas1.c
Enunciado 104
Máx e min de sequência
Estatística
, s/d
anónimo
sem resoluções.
Enunciado 105
Divisível por 3
Números
Exercícios, 1994
Miguel Brito
sem resoluções.
Enunciado 106
Múltiplo (2 números)
Números
Exercícios, 1994
Miguel Brito
sem resoluções.
Enunciado 107
Cálculo do vencimento a partir de parcelas variáveis
Números
Exercícios, 1994
Miguel Brito
Codifique em 'C'
Resoluções:
1. venc.83p
Enunciado 108
Saudação aleatória
strings
Exercícios, 1994
Miguel Brito
sem resoluções.
Enunciado 109
Função
Números
Ficha de problemas, 2001
Dias, M., Martins, F.

sem resoluções.
Enunciado 110
Cadeias de Caracteres - Anagramas I - Construção
strings
Colectânea do NDIG, 1996
Colectânea do NDIG
sem resoluções.
Enunciado 111
Cadeias de Caracteres - Anagramas II - Verificação
strings
Colectânea do NDIG, 1996
Colectânea do NDIG
sem resoluções.
Enunciado 112
Cadeias de Caracteres - Nomes de pessoas
strings
Colectânea do NDIG, 1996
Colectânea do NDIG
"nOme1 NoME2 ApelIDo1 ApELido2 dA ApeliDo3 E ApeLiDo4"
em
"Nome1 Nome2 Apelido1 Apelido2 da Apelido3 e Apelido4"
isto é, converta as letras em maiúsculas ou minúsculas de modo a obter o nome escrito com as regras usuais.
sem resoluções.
Enunciado 113
Determinação do nº de moedas necessário para perfazer uma dada quantia
Números
Exercícios, 1994
Miguel Brito
sem resoluções.
Enunciado 114
Trocos
Colectânea do NDIG, 1996
Colectânea do NDIG
Notas em circulação : 500$, 1000$, 2000$, 5000$, 10000$
Moedas em circulação: 1$, 2$5, 5$, 10$, 20$, 50$, 100$, 200$
sem resoluções.
Enunciado 115
Números de 4 algarismos
Números
Colectânea do NDIG, 1996
Colectânea do NDIG
sem resoluções.
Enunciado 116
Euclides - Máximo Divisor Comum
Colectânea do NDIG, 1996
Colectânea do NDIG
sem resoluções.
Enunciado 117
Classificação de notas
Números
Exercícios, 1994
Miguel Brito
sem resoluções.
Enunciado 118
Área de um triângulo
Geometria
Ciência dos Computadores - Uma abordagem algorítmica, pág. 85, 1983
Tremblay, Bunt
sem resoluções.
Enunciado 119
Classificação de triângulos
Geometria
Ciência dos Computadores - Uma abordagem algorítmica, pág. 85, 1983
Tremblay, Bunt
Se A <= B + C Nenhum triângulo é formado Se A2 = B2 + C2 Um triângulo rectângulo é formado Se A2 > B2 + C2 Um triângulo obtusângulo é formado Se A2 < B2 + C2 Um triângulo acutângulo é formado
sem resoluções.
Enunciado 120
Indústrias Poluentes
Números
Ciência dos Computadores - Uma abordagem algorítmica, pág. 85, 1983
Tremblay, Bunt
sem resoluções.
Enunciado 121
Raposas e coelhos
Simulação
A Chave para o Mundo dos Computadores, Publipress Editora, 1984
Lohberg, Lutz
Raposasn+1 = Raposasn + Raposasn(Coelhosn/5 -30)/100
| Resoluções: 1. rapcoe.bas |
|
Enunciado 122 Espécies animais |
Simulação
A Chave para o Mundo dos Computadores, Publipress Editora, 1984 Lohberg, Lutz |
Neste problema vamos simular a evolução do número de animais de uma dada espécie.
Podemos dizer que a taxa de nascimento é tal que num determinado período, e se não houvesse outros factores, o número de animais dessa espécie aumentaria 25%;
sem resoluções.
|
Enunciado 123 Números |
Fundamental da Programação em 'C', pág. 59, 1998 Sampaio, I. e Sampaio, A. |
Elabore um programa que escreva os n primeiros cubos, segundo o teorema de Nicomachus. Exemplo: Para n=4 (13, 23, 33, 43) virá
23 = 3+5
33 = 7+9+11
43 = 13+15+17+19
| Resoluções: 1. Cubos.83p |
|
Enunciado 124 Calendário |
A Chave para o Mundo dos Computadores, Publipress Editora, 1984 Lohberg, Lutz |
O calendário que utilizamos foi definido em 1538, a pedido do Papa Gregório XIII. Sabendo que o dia 1 de Abril de 1700 foi uma terça feira, é possível reconstruir todo o calendário, e saber em que dia da semana calhou/calha uma determinada data. Contrua uma programa que dada uma data na forma dia, mês, ano, determine o dia da semana correspondente.
| Resoluções: 1. CalGreg.xls 2. CalGReg.htm |
|
Enunciado 125 Ordem decrescente (4 números) |
Números
Exercícios, 1994 Miguel Brito |
sem resoluções.
|
Enunciado 126 Eratóstenes - Nºs. primos |
Colectânea do NDIG, 1996 Colectânea do NDIG |
O algoritmo de Eratóstenes para a determinação de números primos é também chamado "Crivo de Eratóstenes". A ideia base é a do cálculo dos múltiplos de ......
sem resoluções.
|
Enunciado 127 Crivo de Eratóstenes |
Números
Ciência dos Computadores - Uma abordagem algorítmica, pág. 121, 1983 Tremblay, Bunt |
O crivo de Eratóstenes, nome tirado de um astrônomo e geógrafo grego do terceiro século, é uma técnica para gerar números primos. Iniciamos escrevendo todos os inteiros ímpares de 3 a N, eliminando então cada terceiro elemento após o 3, cada quinto elemento após o 5, e assim por diante até que todos os múltiplos, dos ímpares inteiros menores que ÖN (raiz de N) tenham sido eliminados. Os inteiros restantes na lista são exactamente os números primos entre 3 e N. Preparar uma algoritmo para gerar os números primos de 3a 1000, utilizando a técnica do crivo.
sem resoluções.
|
Enunciado 128 Números primos |
Números
Ficha de problemas, 2001 Dias, M., Martins, F. |
Desenvolva uma subrotina para determinar se um dado número inteiro, n, é número primo. Use o seguinte algoritmo:
sem resoluções.
|
Enunciado 129 Totoloto |
Colectânea do NDIG, 1996 Miguel Brito |
Elabore um Algoritmo que simule a extracção de 6 números do Totoloto (os n.ospodem sair repetidos). Codifique em 'C'
sem resoluções.
|
Enunciado 130 Máximo de 10 números |
Colectânea do NDIG, 1996 Miguel Brito |
Elabore um Algoritmo que determine o máximo de uma sequência de 10 números. Codifique em 'C'.
sem resoluções.
|
Enunciado 131 Múltiplos de 3 |
Números
Colectânea do NDIG, 1996 Miguel Brito |
Elabore um Algoritmo que calcule os múltiplos de 3, compreendidos no intervalo entre 6 e um dado limite superior. Codifique em 'C'.
sem resoluções.
|
Enunciado 132 Expressão complexa |
Números
Ficha de problemas, 2001 Dias, M., Martins, F. |
Desenvolva uma subrotina que calcule a seguinte expressão
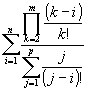
sem resoluções.
|
Enunciado 133 Números |
Ciência dos Computadores - Uma Abordagem Algorítmica, pág. 71, 1981 Tremblay & Bunt |
O custo de seguro contra granizo numa comunidade típica de fazendeiros é 3.5% do vlor de cobertura solicitado por acre, multiplicado pelo número de acres plantados. Supondo que as possibilidades de colheitas sejam limitadas a trigo, aveia e cevada, preparar um algoritmo para ler a cobertura desejada e o número de acres plantados para cada uma das três plantações e calcular o custo total do prémio do seguro para este cliente.
sem resoluções.
|
Enunciado 134 Factorial |
Colectânea do NDIG, 1996 Miguel Brito |
Elabore um Algoritmo que calcule o Factorial de um nº. Codifique em 'C'.
| Resoluções: 1. fac0.bas 2. fac1.bas 3. fac2.bas 4. Factjp.c |
|
Enunciado 135 Números e seus divisores |
Números
Colectânea do NDIG, 1996 Colectânea do NDIG |
Os números podem classificar-se em reduzidos, perfeitos ou abundantes conforma sejam inferiores, iguais ou superiores à soma dos seus divisores (excluindo o próprio número).
Escreva um programa que:
- Classifique os números de 1 a 1000 de acordo com o critério anterior
- Determine, para o mesmo intervalo, quantos números existem em cada classe.
| Resoluções: 1. Rpa1000.83p 2. Rpa1000.cat |
|
Enunciado 136 Números amigos |
Números
Colectânea do NDIG, 1996 Colectânea do NDIG |
Dois números inteiros, X, Y, dizem-se amigos quando a soma dos divisores de X é igual a Y e a soma dos divisores de Y é igual a X. Escreva um programa que determine todos os (pares de) números amigos menores que 20000
| Resoluções: 1. Amigos.bas 2. Amigos0.c 3. Nsamigos.cat |
|
Enunciado 137 Erros em programas |
Ciência dos Computadores - Uma abordagem algorítmica, pág. 102., 1983 Tremblay, Bunt |
Nota: Determine também quantos erros cometeu ao longo das treze semanas.
sem resoluções.
|
Enunciado 138 Números |
Introdução à Informática (2ª Edição), pág. 256, 1997 Rocha, N. P., Ramos, F. M., Oliveira, J. L. |
Escreva um programa que leia um inteiro e que, consoante o número seja positivo ou negativo escreva no monitor `POS´ ou `NEG´ respectivamente.
sem resoluções.
|
Enunciado 139 Determinação dos N primeiros múltiplos de 3 |
Colectânea do NDIG, 1996 Miguel Brito |
Elabore um Algoritmo que calcule os primeiros N múltiplos de 3, sendo N fornecido pelo utilizador. Codifique em 'C'.
sem resoluções.
|
Enunciado 140 Primeiros N números de Fibonacci |
Colectânea do NDIG, 1996 Miguel Brito |
Elabore um Algoritmo que apresente os primeiros N números de Fibonacci (N fornecido pelo utilizador). Fn+2 = Fn+1 + Fn, F0=0 e F1=1 (n => 0). Codifique em 'C'.
| Resoluções: 1. Primnfib.cat |
|
Enunciado 141 Números de Fibonacci menores que N |
Colectânea do NDIG, 1996 Miguel Brito |
Elabore um Algoritmo que apresente os números de Fibonacci inferiores a um dado N. Fn+2 = Fn+1 + Fn, F0=0 e F1=1 (n => 0). Codifique em 'C'.
sem resoluções.
|
Enunciado 142 Primeiros M múltiplos de N |
Colectânea do NDIG, 1996 Miguel Brito |
Elabore um Algoritmo que calcule os primeiros M múltiplos de um dado n.º N, sendo M e N fornecidos pelo utilizador. Codifique em 'C'.
sem resoluções.
|
Enunciado 143 Somatório de sequência de números |
Números
Colectânea do NDIG, 1996 Miguel Brito |
Elabore um Algoritmo que calcule o somatório de uma sequência de N números. N também é pedido ao utilizador. Codifique em 'C'.
| Resoluções: 1. snn.ppt 2. Snn.c |
|
Enunciado 144 Média de sequência de números |
Estatística
Colectânea do NDIG, 1996 Miguel Brito |
Elabore um Algoritmo que calcule a média de uma sequência de números. Codifique em 'C'.
sem resoluções.
|
Enunciado 145 Determina mínimo múltiplo comum de dois números |
Números
Colectânea do NDIG, 1996 Miguel Brito |
Elabore um Algoritmo que dados dois números calcule o seu mínimo múltiplo comum. Codifique em 'C'.
sem resoluções.
|
Enunciado 146 Pontos de uma recta |
Geometria
Colectânea do NDIG, 1996 Miguel Brito |
Elabore um Algoritmo que dada a equação de uma recta na forma Y = mX + b, calcule os valores de Y para valores de X entre 0 e 50, de 5 em 5. Codifique em 'C'.
sem resoluções.
|
Enunciado 147 Percentagem de valores superiores a 10 |
Estatística
Colectânea do NDIG, 1996 Miguel Brito |
Elabore um Algoritmo que dada uma sequência de números inteiros positivos terminada por 0, calcule a percentagem correspondente aos valores superiores a 10 (o 0 não conta para efeitos de cálculo!). Codifique em 'C'.
| Resoluções: 1. Sup10.cat |
|
Enunciado 148 Divisores de um número |
Colectânea do NDIG, 1996 Miguel Brito |
Elabore um Algoritmo que calcule os divisores de um n.º (o resto da divisão do n.º por um seu divisor é 0). Codifique em 'C'.
sem resoluções.
|
Enunciado 149 Jogo hi-lo repetido 4 vezes |
Jogos
EC; PP, 1997 Trabalho prático (97/98) |
Considere o seguinte jogo com dois jogadores, o jogador A e o jogador B.
O jogador A pensa num número inteiro {0..100} e o jogador B tem 10 tentativas para o adivinhar. Após cada tentativa do jogador B, o jogador A indica se a tentativa foi alta, baixa ou se acertou.
Depois de B ter acertado ou excedido o número de tentativas, os pápeis invertem-se e será a vez de A adivinhar o número que B pensa.
Será vencedor o jogador que tiver acertado, em menos tentativas, nos números correctos, num total de 4 jogos.
Projecte e escreva um programa que implemente este jogo, sendo o computador um dos jogadores.
O programa terá de indicar, no final dos 4 jogos, qual dos jogadores foi o vencedor, e apresentar um resumo com os números pensados, qual dos jogadores jogava como adivinhador e quantas tentativas efectuou.
sem resoluções.
|
Enunciado 150 Custo de um seguro |
Números
Ciência dos Computadores - Uma Abordagem Algorítmica, pág. 71, 1981 Tremblay & Bunt |
| Altura do prédio (m) | Tempo gasto para atingir o solo (s) |
sem resoluções.
|
Enunciado 151 Efeito Doppler |
Números
Ciência dos Computadores - Uma Abordagem Algorítmica, pág. 71, 1981 Tremblay & Bunt |
Embora a velocidade da luz seja constante, não importando a velocidade relativa da fonte e do observador, o comprimento de onda e a frequência mudam - um efeito previsto pela primeira vez por Johann Doppler e conhecido como o "Efeito Doppler". O comprimento de onda l emitido por uma fonte movendo-se em direcção ao observador com uma velocidade v é comprimido por uma quantidade Dl, que é dada pela fórmula
= 10-3 cm
sem resoluções.
|
Enunciado 152 Determinação de máx., min. e media |
Estatística
Colectânea do NDIG, 1996 Colectânea do NDIG |
Dado um vector de números, escreva um programa que determine:
sem resoluções.
|
Enunciado 153 Ordenação de vectores |
Vectores
Colectânea do NDIG, 1996 Colectânea do NDIG |
sem resoluções.
|
Enunciado 154 Padrões em vectores |
Vectores
Colectânea do NDIG, 1996 Colectânea do NDIG |
sem resoluções.
|
Enunciado 155 Totoloto |
Simulação
Exercícios, 1996 Miguel A. Brito |
Elabore um Algoritmo que simule a extracção dos 6 números do Totoloto, garantindo que não há repetidos. Codifique em 'C'.
Descrições de resoluções: c:\pimenta\iiee\bedepro\G55_.htm c:\pimenta\iiee\bedepro\G55_.htm c:\pimenta\iiee\bedepro\G55_.htm c:\pimenta\iiee\bedepro\G55_.htm
| Resoluções: 1. G55_.c 2. G55_.c 3. G55_.c 4. G55_.c 5. Totolo1.bas 6. Totolo2.bas 7. Totolo3.bas 8. Totoloto.m 9. Totoloto.xls 10. Totoloto2.xls 11. Totolo1.cat 12. Totolo2.cat |
|
Enunciado 156 Totoloto |
Jogos
Colectânea do NDIG, 1996 Colectânea do NDIG |
Detalhe o algoritmo e escreva um programa que:
sem resoluções.
|
Enunciado 157 Notas de alunos |
Estatística
Exercícios, 1996 Miguel A. Brito |
Elabore um Algoritmo que dadas as notas de um conjunto de alunos, apresente o n.º de ocorrências de cada uma das notas; em vez de apresentar o n.º de ocorrências de todas as notas entre 0 e 20 apresente apenas as que se situem entre a nota mínima e a nota máxima. No fim, apresente os seguintes valores estatísticos: nota máxima; nota mínima; n.º de negativas (< 10); percentagem de positivas; média das notas; média das notas positivas; n.º de notas superiores à média. Codifique em 'C'.
sem resoluções.
|
Enunciado 158 Ordenação de uma sequência de nomes |
strings
Exercícios, 1996 Miguel A. Brito |
Elabore um algoritmo que dada uma sequência de nomes, os apresente por ordem alfabética. Codifique em 'C'.
sem resoluções.
|
Enunciado 159 Estatística |
Estatística
Exercícios, 1996 Miguel A. Brito |
Dada uma sequência de números, determine a percentagem daqueles que são: superiores à média dos elementos que a constituem; inferiores ao antepenúltimo elemento da sequência. Codifique em 'C'.
sem resoluções.
|
Enunciado 160 Factoriais menores que... |
Estatística
Exercícios, 1996 Miguel A. Brito |
sem resoluções.
|
Enunciado 161 Factoriais por ordem decrescente... |
Números
Exercícios, 1996 Miguel A. Brito |
sem resoluções.
|
Enunciado 162 Máximo divisor comum |
Exercícios, 1996 Miguel A. Brito |
sem resoluções.
|
Enunciado 163 Números perfeitos |
Números
Exercícios, 1996 Miguel A. Brito |
Elabore um Algoritmo que calcule todos os números perfeitos inferiores a um dado valor (um n.º perfeito é aquele que é igual à soma dos seus divisores, excluindo ele próprio). Codifique em 'C'.
| Resoluções: 1. Nperfs.83p |
|
Enunciado 164 Cálculo do sub-factorial de um N |
Números
Exercícios, 1996 Miguel A. Brito |
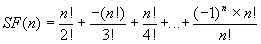 .
.Codifique em 'C'.
| Resoluções: 1. Sf.m 2. Sf.mws |
|
Enunciado 165 Produção mensal |
Estatística
Exercícios, 1996 Miguel A. Brito |
Elabore um algoritmo que baseando-se nos valores de produção mensal de uma fábrica de automóveis num dado ano, calcule e apresente: os valores mensais acumulados de produção ao longo do ano; o mês em que foi atingida metade da produção anual. Codifique em 'C'.
sem resoluções.
|
Enunciado 166 Estatística sobre N números |
Estatística
Exercícios, 1996 Miguel A. Brito |
Elabore um Algoritmo que depois de ler uma sequência de N números (N também pedido ao utilizador), apresente os seguintes resultados: máximo, mínimo, somatório, a quantidade de números superiores a 10, a percentagem de valores superiores a 10, a média, a média dos valores superiores a 10. Codifique em 'C'.
sem resoluções.
|
Enunciado 167 Estatística sobre 30 números |
Estatística
Exercícios, 1996 Miguel A. Brito |
| Resoluções: 1. En167.cat |
|
Enunciado 168 Números aleatórios |
Números
Exercícios, 1996 Miguel A. Brito |
Elabore um Algoritmo que apresente uma sequência de N números aleatórios, em que cada n.º não pode ser igual a nenhum dos dois imediatamente anteriores. N deve ser pedido ao utilizador. Codifique em 'C'.
sem resoluções.
|
Enunciado 169 hi-lo |
Jogos
Exercícios, 1996 Miguel A. Brito |
Elabore um Algoritmo que implemente o jogo "hi-lo". A finalidade do jogo é que o utilizador acerte num número entre 1 e 100, escolhido aleatoriamente pelo programa. A cada palpite do utilizador, o programa deve responder indicando se este é inferior ou superior ao número escondido. Quando o utilizador acertar, o programa deve dar-lhe os parabéns e indicar em quantas jogadas acertou. Codifique em 'C'.
sem resoluções.
|
Enunciado 170 hi-lo |
Jogos
A Chave para o Mundo dos Computadores, Publipress Editora, 1984 Lohberg, Lutz |
Elabore um Algoritmo que implemente o jogo "hi-lo". A finalidade do jogo é que o utilizador acerte num número entre 0 e 99, escolhido aleatoriamente pelo programa. A cada palpite do utilizador, o programa deve responder indicando se este é inferior ou superior ao número escondido, assim como um comentário - aleatório - de motivação ao jogador. O programa deve permitir um máximo de 8 tentativas.
| Resoluções: 1. hi-lo0.ppt 2. Hilo.c 3. Hilo.bas 4. hilomn.c |
|
Enunciado 171 hi-lo |
Jogos
A Chave para o Mundo dos Computadores, Publipress Editora, 1984 Lohberg, Lutz |
Elabore um Algoritmo que implemente o jogo "hi-lo". A finalidade do jogo é que o computador acerte num número entre 1 e 127, escolhido utilizador. A cada palpite do computador, o utilizador deve responder indicando se o palpite é inferior, igual ou superior ao número escolhido pelo utilizador. Caso o utilizador faça batota, o computador deverá detectar essa situação e explicar a situação ao utilizador.
| Resoluções: 1. Hilo1.c |
|
Enunciado 172 O jogo do nim |
Jogos
A Chave para o Mundo dos Computadores, Publipress Editora, 1984 Lohberg, Lutz |
O jogo do Nim é jogado por dois jogadores, retirando fósforos de um monte de fósforos. No início do jogo, os jogadores combinam qual o número inicial de fósforos do monte, e qual o nº máximo que cada jogador pode retirar em cada jogada. Depois do sorteio do primeiro a jogar, cada um dos jogadores, alternadamente, retira o nº de fósforos que desejar, com um mínimo de 1 e o maximo previamente acordado. Quem tirar o último fósforo, perde. Construa um programa que jogue nim contra um jogador humano.
sem resoluções.
|
Enunciado 173 Séries de 5 dados |
Simulação
Exercícios, 1996 Miguel Brito |
Elabore um Algoritmo que simule o lançamento de séries de 5 dados; no fim de cada série, deve perguntar ao utilizador se quer outra série, e proceder de acordo com a resposta. Codifique em 'C'.
sem resoluções.
|
Enunciado 174 Série de números |
Números
Exercícios, 1996 Miguel Brito |
Elabore um Algoritmo que leia uma sequência de números, e os mostre por ordem inversa. Codifique em 'C'.
sem resoluções.
|
Enunciado 175 Percentagem do total |
Estatística
Exercícios, 1996 Miguel Brito |
Elabore um Algoritmo que dada uma sequência de números, indique qual a percentagem que cada um representa em relação ao total. Codifique em 'C'.
| Resoluções: 1. Pertot.83p |
|
Enunciado 176 Estatística de classificações |
Estatística
Exercícios, 1996 Miguel Brito |
Elabore um Algoritmo que dadas as notas de um conjunto de alunos, através de uma sequência terminada por um nº negativo, calcule os seguintes valores estatísticos: nota máxima; nota mínima; nº de positivas (> 10); percentagem de negativas; média das notas; média das notas positivas. Codifique em 'C'.
sem resoluções.
|
Enunciado 177 Temperaturas de cidades |
Estatística
Exercícios, 1996 Miguel Brito |
Elabore um Algoritmo que dado um conjunto de temperaturas de cidades portuguesas, identificadas por um n.º de ordem, indique quais as que têm temperatura superior à média do país. Codifique em 'C'.
sem resoluções.
|
Enunciado 178 Fichas de jogadores |
Fichas
Ciência dos Computadores - Uma abordagem algorítmica, pág. 121., 1983 Tremblay, Bunt |
sem resoluções.
|
Enunciado 179 Temperaturas de cidades |
Estatística
Exercícios, 1996 Miguel Brito |
Elabore um Algoritmo que dado um conjunto de temperaturas de cidades portuguesas, identificadas por um n.º de ordem, indique quais as que têm temperatura superior à média do país mas ordenadas por ordem decrescente de temperatura. Codifique em 'C'.
sem resoluções.
|
Enunciado 180 Número por extenso |
Strings
Exercícios, 1996 Colectânea do NDIG |
Detalhe um algoritmo e escreva um programa que, dado um número inteiro, escreva o seu valor por extenso.
sem resoluções.
|
Enunciado 181 Trocos de moedas |
Números
Ciência dos Computadores - Uma abordagem algorítmica, pág. 121., 1983 Tremblay, Bunt |
sem resoluções.
|
Enunciado 182 Master-mind |
Jogos
Exercícios, 1996 Colectânea do NDIG |
Elabore um algoritmo e escreva um programa que jogue Master-Mind.
sem resoluções.
|
Enunciado 183 Master-mind |
Jogos
Exercícios, 1996 Colectânea do NDIG |
Elabore um Algoritmo que permita ao utilizador jogar “Master Mind”; o programa deve gerar aleatoriamente a combinação a descobrir, e depois responder a cada palpite do utilizador, indicando o n.º de elementos certos na casa certa, e o n.º de elementos certos na casa errada. O número de elementos e de cores a usar, deve ser pedido ao utilizador no início do programa (os valores típicos são 4 e 6 respectivamente). O jogador deve ter a possibilidade de desistir! Quando o utilizador acertar na combinação gerada, o programa deve indicar o n.º de jogadas em que o fez. Codifique em 'C'.
sem resoluções.
|
Enunciado 184 Jogo de Sorte |
Jogos
Exercícios, 1996 Colectânea do NDIG |
Escreva um programa que, utilizando a geração de números aleatórios, jogue o seguinte jogo:
sem resoluções.
|
Enunciado 185 Vector A |
Vectores
Ciência dos Computadores - Uma abordagem algorítmica, pág. 132., 1983 Tremblay, Bunt |
sem resoluções.
|
Enunciado 186 Mil portas |
Números
Exercícios, 1996 Colectânea do NDIG |
Considere um corredor com mil portas, numeradas de 1 a 1000, que se encontram todas fechadas. Por esse corredor passarão mil pessoas, que modificarão o estado da(s) porta(s) cujo número seja múltiplo do seu número de passagem: a pessoa com o número 3 modificará o estado (fechará se estiverem abertas ou abrirá se estiverem fechadas) as portas nos. 3, 6, 9, 12,.... e a pessoa nº 7 fará o mesmo às portas 7, 14, 21, etc...
Construa um algoritmo e escreva um programa que permita saber quantas são as portas abertas e quantas são as portas fechadas após a passagem da milésima pessoa.
| Resoluções: 1. Mportas1.c |
|
Enunciado 187 Vector A de números reais |
Vectores
Ciência dos Computadores - Uma abordagem algorítmica, pág. 132., 1983 Tremblay, Bunt |
sem resoluções.
|
Enunciado 188 Vector A de números reais |
Vectores
Ciência dos Computadores - Uma abordagem algorítmica, pág. 133., 1983 Tremblay, Bunt |
Repetir o exercício anterior e obter a menor diferença entre dois elementos consecutivos.
sem resoluções.
|
Enunciado 189 Tráfego entre cidades |
Simulação
Exercícios, 2003 Pedro Pimenta |
A seguinte matriz indica o custo de transporte unitário entre as cidades indicadas como A, B, C, D, E, F, G, H, I e J.
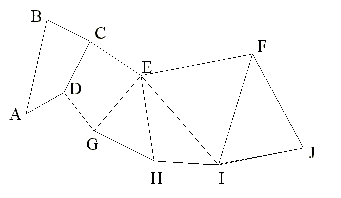 |
|
sem resoluções.
|
Enunciado 190 Fluir de tráfego |
Simulação
Computadores, Publipress Editora, 1984 Lohberg, Lutz |
O diagrama esquematiza as condições de tráfego entre o ponto A e ponto S.
Os rectângulos representam troços de caminho livre, que o condutor percorre num tempo fixo. As ovais representam semáforos, com o tempo de espera máximo indicado. Os losangos (M e N) representam bifurcações, em que o condutor escolhe entre dois caminhos alternativos, de acordo com as percentagens indicadas. Construa um programa que simule T trajectos entre A e S, e indique o trajecto mais rápido, o mais lento e a média dos tempos dos trajectos.
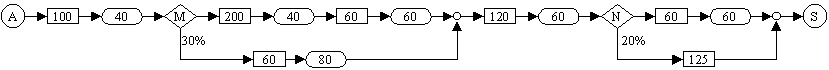
| Resoluções: 1. Trafego.83p 2. Trafego.bas |
|
Enunciado 191 Departamento de Pesca |
Fichas
Ciência dos Computadores - Uma abordagem algorítmica, pág. 116., 1983 Tremblay, Bunt |
Os pescadores profissionais são obrigados a informar mensalmente ao Departamento de Pesca do Ministério sua produção. Estes dados são analisados regularmente para determinar o crescimento ou a redução das várias espécies de peixe e indicar qualquer possível problema. Com estes dados é preparado um cartão contendo as seguintes informações:
Este exemplo indica que, na região 16, um total de 20485 dourados foram apanhados num determinado mês deste ano e que 18760 dourados foram apanhados no mesmo mês do último ano. Preparar um algoritmo para ler um conjunto de cartões com estes dados (O último cartão tem uma região com número negativo) e indicar qualquer crescimento ou redução anormal do número de peixes. Um crescimento ou redução anormal é definido como o caso onde a percentagem de mudança excede os 30%. A mudança percentual é definida como

sem resoluções.
|
Enunciado 192 Governo das ilhas Oba-oba |
Fichas
Ciência dos Computadores - Uma abordagem algorítmica, pág. 117, 1983 Tremblay, Bunt |
O governo das ilhas Oba-Oba institui um controlo de preços e salários logo após a sua eleição. O Primeiro-Ministro recebeu de seus conselheiros económicos uma previsão, baseada nas tendências actuais, de que os salários continuarão a aumentar anualmente de 5%, o custo de vida e de serviços de 10%, e os impostos de 15%. Seus conselheiros políticos informam que, se os impostos mais o custo de vida subirem mais do que 75% do salário anual para um número sigificativo dos cidadãos, ele terá problemas nas próximas eleições (esperadas em 3 anos) e que, se isto atingir 80%, ele se verá realmente em apuros. O Primeiro-Ministro tem colectados e colocados em cartões o salário anual, os impostos e o custo de vida e serviços para uma amostra tomada dos seus eleitores. Preparar um algoritmo para determinar o número e a percentagem dos cidadãos estudados que caem nas categorias de 75% e 80% já descritas. O número de pessoas da amostra é desconhecido. Utilizar o método fim-de-arquivo para terminar a leitura de dados.
sem resoluções.
|
Enunciado 193 Ordenação de uma sequência de nomes |
Strings
Exercícios, 1996 Miguel A. Brito |
Elabore um algoritmo que permita ao utilizador fazer a manutenção dos dados referentes aos artigos que tem em "stock". O programa deverá apresentar ao utilizador um menu no qual este poderá escolher a opção que pretende. As opções disponíveis, deverão ser as de inserir, alterar, remover e consultar um artigo, e ainda listar todos os artigos existentes, cujo stock seja superior a um dado valor; no fim da listagem, deverá ser apresentado o valor total do "stock" (S(preço ´ quantidade)) correspondente aos artigos listados e o correspondente à totalidade dos artigos. Cada artigo é identificado por um código, que permite aceder à quantidade existente e ao valor unitário. Codifique em 'C'.
sem resoluções.
|
Enunciado 194 Número primo |
Números
Ciência dos Computadores - Uma abordagem algorítmica, pág. 103., 1983 Tremblay, Bunt |
Um número é, por definição, primo se ele não tem divisores, excepto 1 e ele próprio. Preparar um algoritmo para ler um número e determinar se ele é ou não um número primo.
sem resoluções.
|
Enunciado 195 Determinação dos n primeiros nos primos |
Números
Fundamental da Programação em 'C', pág. 59, 1998 Sampaio, I. e Sampaio, A. |
Escreva um programa que verifique se um dado número x é, ou não primo considerando que um número é primo se for divisível apenas por si e pela unidade, e que o maior divisor útil é 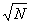
sem resoluções.
|
Enunciado 196 Números primos |
Números
Colectânea do NDIG, 1996 Colectânea do NDIG |
sem resoluções.
|
Enunciado 197 Primos entre 100 e 200 |
Números
Introdução à Informática (2ª Edição), pág. 257, 1997 Rocha, N. P., Ramos, F. M., Oliveira, J. L. |
Escreva um programa em Turbo Pascal que apresente no ecrã todos os números primos existentes entre 100 e 200.
Nota: Um número primo sé é divisível por 1 e por si mesmo.
sem resoluções.
|
Enunciado 198 Início e incremento até 100 |
Números
Introdução à Informática (2ª Edição), pág. 257, 1997 Rocha, N. P., Ramos, F. M., Oliveira, J. L. |
Escreva um programa em Turbo Pascal que comece por ler um VALOR INICIAL entre 1 e 10, e um INCREMENTO entre 1 e 5. Depois da leitura dos dados, o programa deverá escrever no ecrã uma tabela de uma série de números que começa no VALOR INICIAL, acaba em 100, e em que cada número é o resultado da adição do número anterior com o INCREMENTO.
sem resoluções.
|
Enunciado 199 Problema com potências |
Números
Colectânea do NDIG, 1996 Colectânea do NDIG |
Encontre o menor c que admite 10 soluções diferentes da igualdade (a, b e c Î N):
sem resoluções.
|
Enunciado 200 Problema com potências |
Números
Colectânea do NDIG, 1996 Colectânea do NDIG |
Encontre 4 números inteiros tais que (Fermat J)
sem resoluções.
|
Enunciado 201 Problema com potências |
Números
Colectânea do NDIG, 1996 Colectânea do NDIG |
Encontre a, b, c, d e e tais que
sem resoluções.
|
Enunciado 202 Repartição Pública |
Vectores
Exercícos, 1996 Miguel A. Brito |
Considere uma repartição pública de requisição de instalação de serviços. O atendimento está dividido em três guichets cujas filas de espera, por limitações físicas do próprio edifício, estão bastante distantes umas das outras. Cada pessoa que entra no edifício retira uma senha de atendimento e segue para a fila de um dos três guichets disponíveis. Dada a distância física entre os guichets não é possível respeitar a ordem de atendimento em relação à de chegada. No entanto é possível, através do n.º da senha que se tira à entrada, respeitar essa ordem para efeitos de instalação do serviço. Assim, pretende-se construir um programa em que, dados três pares de arrays (vectores) cuja informação representa a pessoa (pelo B.I.) e o n.º da senha, fazer a junção dos três vectores num único array de B.I.s ordenado pelo n.º de senha. As senhas não aparecem todas, porque normalmente há desistências. Como cada uma das três filas já está ordenada, basta ir retirando de cada uma o elemento com n.º de senha mais baixo e colocar o respectivo n.º de B.I. no array de requisição de serviços.
sem resoluções.
|
Enunciado 203 Registo de notas |
Vectores
Exercícos, 1996 Miguel A. Brito |
Elabore um algoritmo que permita registar as notas dos alunos de Engenharia Electrónica Industrial à disciplina de Programação de Computadores I. O programa deve ter informação sobre o número, nome, e notas dos 3 exames. Deve permitir ao utilizador introduzir, consultar e alterar as notas de um aluno, ter uma opção para alterar as notas de todos os alunos existentes, e ainda tirar listagens por ordem de número de aluno e por ordem alfabética, conforme pedido do utilizador; para cada aluno, as listagens deverão indicar se está aprovado ou não, sabendo que para isso deverá ter uma das três notas > 10. Codifique em 'C'.
sem resoluções.
|
Enunciado 204 Cumprimento ao Utilizador |
Strings
Exercícos, 1996 Miguel A. Brito |
Elabore um algoritmo que pergunte o nome ao utilizador, e responda aleatoriamente «"Olá ", nome, "!"», «"Como está ", nome, "?"» ou «"Prazer em vê-lo ", nome, "!"»; depois de cumprimentar o utilizador, deve pedir outro nome, e assim sucessivamente até que a resposta seja "ninguém". Se o nome introduzido for igual a um dos últimos 10 nomes anteriormente introduzidos, em vez de cumprimentar, responder "Outra vez, ", nome, "?". Codifique em 'C'.
sem resoluções.
|
Enunciado 205 Consumo de Gasolina |
Números
Ciência dos Computadores - Uma abordagem algorítmica, pág. 103., 1983 Tremblay, Bunt |
Um motorista acaba de retornar de um feriado prolongado. Em cada parada de reabastecimento ele registou a leitura do seu odômetro e a quantidade de gasolina comprada (suponha que ele tenha enchido o tanque de cada vez). Além disso, suponha também que ele tenha enchido o tanque antes de partir e imediatamente antes de retornar, registando as leituras do odômetro em cada posto. Preparar um algoritmo para ler em primeiro lugar o número total de reabastecimentos feitos (incluindo o primeiro e o último) e, a seguir, os dados registados relativos à compra de gasolina e calcular
sem resoluções.
|
Enunciado 206 Quadrado mágico |
Números
Computadores, Publipress Editora, 1984 Lohberg, Lutz |
|
Um quadrado mágico é constituído pelos primeiros N2 números num quadrado de forma a que a soma dos elementos em cada linha, e em cada coluna, e em cada diagonal seja igual.
Na figura ao lado está representado um quadrado mágico para N = 5. Só são conhecidas regras determinísticas para construir quadrados mágicos com um número ímpar de elementos. Adam Riese, um matemático que viveu entre 1492 e 1559, descreveu assim essas regras: |  |
|
|
sem resoluções.
|
Enunciado 207 Termos de uma série |
Números
Ciência dos Computadores - Uma abordagem algorítmica, pág. 102., 1983 Tremblay, Bunt |
Preparar um algoritmo para calcular a soma da seguinte série de 100 termos:
sem resoluções.
|
Enunciado 208 Números primos |
Números
, s/d Anónimo |
Têm sido feitas várias tentativas para encontrar uma fórmula para gerar números primos. Uma dessas fórmulas é a seguinte: xn = n2 +n + 41. Escreva um programa que gere os vários xn, com n dado pelo Utilizador. Deve também ser indicado se o número gerado é primo ou não.
Sugestão: Construa uma função para determinar se o número é primo ou não.
sem resoluções.
|
Enunciado 209 Decomposição em factores primos |
Números
Fundamental da Programação em 'C', pág. 59, 1998 Sampaio, I. e Sampaio, A. |
Escreva um programa para decompor um número, dado pelo utilizador, nos seus factores primos (produto de números primos que são seus divisores).
sem resoluções.
|
Enunciado 210 Sucessões |
Números
Computadores, Publipress Editora, 1984 Lohberg, Lutz |
Construa um programa que determine o valor das seguintes séries;
sem resoluções.
|
Enunciado 211 Aquiles e a tartaruga |
Números
Ciência dos Computadores - Uma abordagem algorítmica, pág. 102, 1983 Tremblay, Bunt |
O antigo filósofo Zeno é, talvez, melhor conhecido pelo paradoxo de Aquiles e a tartaruga. Aquiles e uma tartaruga disputam uma corrida. Aquiles corre dez vezes mais rápido do que a tartaruga, porém a tartaruga tem 100 metros de vantagem. Pode-se argumentar que Aquiles nunca ultrapassará a tartaruga, pois, quando ele atingir o ponto onde a tartaruga estava, ela já estará um pouco mais à frente. Projetar um algoritmo para utilizar um laço e calcular o tempo no qual Aquiles ultrapassará a tartaruga.
sem resoluções.
|
Enunciado 212 Fichas pessoais |
Fichas
Trabalho prático, (97/98), 1997 EC, LR, JCN, PP |
Projecte e escreva um programa que:
sem resoluções.
|
Enunciado 213 Fichas de jogadores de futebol |
Fichas
Ciência dos Computadores - Uma abordagem algorítmica, pág. 103, 1983 Tremblay, Bunt |
Suponha que cada time de futebol, participante da Taça de Ouro, tenha uma lista oficial de 23 jogadores. Os times são obrigados a preparar um cartão para cada um dos seus jogadores, com o formato:
nome do jogador, peso, idade
Os dados dos quarenta times são colectados e enviados à CFB (Confederação Brasileira de Futebol) para análise. Um único conjunto de cartões é preparado, com os cartões agrupados por time individual; isto é, os primeiros 23 cartões são do time 1, os próximos 23 do time 2, e assim por diante. Preparar um algoritmo para ler est econjunto de cartões e calcular a seguinte estatística:
sem resoluções.
|
Enunciado 214 Relatório de clientes |
Ciência dos Computadores - Uma abordagem algorítmica, pág. 103, 1983 Tremblay, Bunt |
Um empresa VENDE TUDO, SA, utiliza um computador para preparar relatórios a seus clientes. Para cada cliente um conjunto de cartões de dados é preparado, contendo informações de seus pagamentos e de suas compras no mês. Os dados para cada cliente iniciam com um cartão especial que contém seu nome, endereço e saldo dos meses anteriores. Este cartão é seguido pelos cartões de transacção, contendo o nome do cliente, a descrição da transacção e o seu valor. O valor das compras terá sempre um valor negativo. Uma entrada típica seria:
| O último cartão é um cartão fictício com o nome do cliente 'ULTIMO CARTAO' |
SQN 203 Bloco B
BRASILIA
| PARA: | A. PEDROSA NOVE DE JULHO 704 | |||
| ITEM | PAGAMENTOS | RETIRADAS | TOTAL | |
| DIVIDA | 1000.00 | 1000.00 | ||
| CHEQUE PAGAMENTO | 500.00 | 1500.00 | ||
| COMPRA FRALDAS | 50.00 | 1450.00 | ||
| COMPRA TALCO | 75.00 | 1375.00 | ||
| TAXA SERVICO | .50 | 1374.50 | ||
| JUROS PAGOS | 3.75 | 1378.25 |
sem resoluções.
|
Enunciado 215 Fichas pessoais |
Fichas
Trabalho prático, (97/98), 1997 EC, LR, JCN, PP |
Projecte e escreva um programa que:
2b. o histórico das transacções:
(os detalhes de todas as transacções): pagamento / trocos.
Moedas em circulação: 200$, 100$, 50$, 20$, 10$, 5$, 2$5, 1
sem resoluções.
|
Enunciado 216 Distribuidor de brinquedos |
Estatística
Ciência dos Computadores - Uma abordagem algorítmica, pág. 117, 1983 Tremblay, Bunt |
Um distribuidor de brinquedos fez um acordo de compra de 10000 brinquedos pequenos embalados em caixas de formato rectangular de tamanhos variados. Ele pretende reembalar estas caixas em esferas coloridas de plástico e revendê-las como pacotes surpresa. As esferas são fornecidas com quatro diâmetos diferentes; 10, 15, 20 e 25 cm. Para pedir as esferas, ele precisa saber quantas de cada diâmetro ele necessita. Sabendo que a diagonal de uma caixa rectangular com as dimensões A, B e C, dadas por
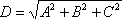
sem resoluções.
|
Enunciado 217 Bingo |
Jogos
Trabalho prático, (97/98), 1997 EC, LR, JCN, PP |
Projecte e escreva um programa que:
sem resoluções.
|
Enunciado 218 Pescaria em S. Paulo |
Números
Ciência dos Computadores - Uma abordagem algorítmica, pág. 102, 1983 Tremblay, Bunt |
Os regulamentos de pesca do Estado de São Paulo impõem um limite no peso total de pesca de um dia. Suponha que você planeja levar o seu terminal portátil de computador em sua próxima pescaria e deseja um programa para calcular quando você excedeu seu limite. Preparar um algoritmo que leia o limite diário (em quilogramas) e, então, leia os valores de entrada um por um (os pesos dos peixes à medida que são apanhados) e imprima uma mensagem no ponto quando este limite é excedido. Um peso de zero indica o fim de entrada. Após o registo de cada peixe, o algoritmo deve imprimir o peso total de peixes obtido até aquele ponto.
sem resoluções.
|
Enunciado 219 Bolsas de Estudo |
Números
Ciência dos Computadores - Uma abordagem algorítmica, pág. 102, 1983 Tremblay, Bunt |
Recomendam-se estudantes para bolsas de estudo em função de seu desempenho anterior. A natureza das recomendações é baseada na seguinte tabela:
| Média | Recomendação |
| > 90% | Altamente recomendado |
| > 80% mas < 90% | Fortemente recomendado |
| > 70% mas < 80% | Recomendado |
| < 70% | Não recomendado |
sem resoluções.
|
Enunciado 220 Aumento de salários |
Números
Ciência dos Computadores - Uma abordagem algorítmica, pág. 107, 1983 Trembay, Bunt |
O Taubaté Esport Club deseja aumentar o salário de seus 20 jogadores registados. O ajuste salarial deve obedecer à seguinte tabela:
| Salário Actual | Acção |
| de 0 a Cr$ 900000 | aumento 20% |
| de Cr$ 900001 a Cr$ 1300000 | aumento 10% |
| de Cr$ 1300001 a Cr$ 1800000 | aumento 5% |
| acima 1800000 | sem aumento |
| Resoluções: 1. En188.c |
|
Enunciado 221 Exames de estudantes |
Números
Ciência dos Computadores - Uma abordagem algorítmica, pág. 108, 1983 Tremblay, Bunt |
Numa classe, são feitos cinco exames (A, B, C, D e E). Pedem-se estatísticas para determinar o número de estudantes que:
sem resoluções.
|
Enunciado 222 Departamento de marketing |
Fichas
Ciência dos Computadores - Uma abordagem algorítmica, pág. 117, 1983 Tremblay, Bunt |
O Departamento de marketing de uma editora está com o problema de calcular o ponto de equilíbrio (despesa = receita) para qualquer livro que ele se propõe a publicar. Este ponto define o número de cópias do livro que devem ser vendidos para que os custos de produção sejam cobertos. Os custos de produção consistem em um custo fixo para a formatação, composição, edição e assim por diante, mais um custo de cópia para impressão, encadernação e outras despesas. Para cada candidato por publicação, é feita uma análise para determinar o número provável de vendas, os custos de produção, baseados principalmente no tamanho do livro (número de páginas), e número de cópias produzidas de acordo com a fórmula:
sem resoluções.
|
Enunciado 223 Departamento de Trânsito |
Fichas
Ciência dos Computadores - Uma abordagem algorítmica, pág. 118, 1983 Tremblay, Bunt |
O Departamento de Trânsito do Estado de São Paulo compilou dados de acidentes de tráfego no último ano. Para cada motorista envolvido num acidente, um cartão foi preparado com as seguintes informações:
sem resoluções.
|
Enunciado 224 Número de dígitos |
Números
Fundamental da Programação em 'C', pág. 76, 1998 Sampaio, I. e Sampaio, A. |
Escreva uma função que retorne o número de dígitos que compõem um número inteiro positivo passado como argumento da função.
sem resoluções.
|
Enunciado 225 Rendimento tributável |
Fichas
Ciência dos Computadores - Uma abordagem algorítmica, pág. 118, 1983 Tremblay, Bunt |
Os tributos de Imposto de Renda de um País "A" são dados pela tabela a seguir:
| Renda Tributável | Taxa |
| $ 654 ou menos | $ 6% $ |
| 654 | 39 + 18 % nos próximos anos 653 |
| 1307 | 157 + 19 % nos próximos anos 1307 |
| 2614 | 405 + 20 % nos próximos anos 1307 |
| 3921 | 667 + 21 % nos próximos anos 2614 |
| 6535 | 1216 + 23 % nos próximos anos 2614 |
| 9149 | 1817 + 25 % nos próximos anos 2614 |
| 11763 | 2470 + 27 % nos próximos anos 2614 |
| 14377 | 3176 + 31 % nos próximos anos 3921 |
| 18298 | 4392 + 35 % nos próximos anos 13070 |
| 31368 | 8966 + 39 % nos próximos anos 19605 |
| 50973 | 16612 + 43 % nos próximos anos 27447 |
| 78420 | 28414 + 47 % nos próximos anos |
sem resoluções.
|
Enunciado 226 Número de dígitos |
Números
Fundamental da Programação em 'C', pág. 76, 1998 Sampaio, I. e Sampaio, A. |
Escreva uma função que devolva o algarismo que está numa dada posição de um número inteiro.
sem resoluções.
|
Enunciado 227 Departamento de Trânsito |
Fichas
Ciência dos Computadores - Uma abordagem algorítmica, pág. 119, 1983 Tremblay, Bunt |
O Departamento de Trânsito de São José dos Campos acumulou informações de excesso de velocidade num determinado período de tempo. O Departamento dividiu a cidade em quatro sectores e deseja estatísticas sobre as violações por excesso de velocidade por quadrante (sector). Para cada violação, é preparado um cartão contendo as seguintes informações:
Veículo | registada (km/h) | limite (km/h) |
sem resoluções.
|
Enunciado 228 Parte inteira |
Números
Fundamental da Programação em 'C', pág. 76, 1998 Sampaio, I. e Sampaio, A. |
Escreva uma função que retorne a parte inteira de um núnero real positivo, passado como argumento.
sem resoluções.
|
Enunciado 229 Tabulação de uma função |
Números
Ciência dos Computadores - Uma abordagem algorítmica, pág. 120, 1983 Tremblay, Bunt |
sem resoluções.
|
Enunciado 230 Mínimo múltiplo comum |
Números
Fundamental da Programação em 'C', pág. 76, 1998 Sampaio, I. e Sampaio, A. |
Desenvolva uma função que calcula o mínimo múltiplo comum de 2 números.
sem resoluções.
|
Enunciado 231 Soma de factores primos |
Números
, 2002 |
Encontre pares de números cuja soma dos seus factores primos seja igual.
sem resoluções.
|
Enunciado 232 Séries exponencial() e sin() |
Números
Fundamental da Programação em 'C', pág. 76, 1998 Sampaio, I. e Sampaio, A. |
Desenvolva funções para o cálculo das seguintes séries:
sem resoluções.
|
Enunciado 233 Companhia de Pulverização |
Números
Ciência dos Computadores - Uma abordagem algorítmica, pág. 120, 1983 Tremblay, Bunt |
A Companhia de Pulverização Faz Tudo Ltda. utiliza aviões para pulverizar lavouras. Os custos de pulverização dependem do tipo de praga e da área contratada conforme o esquema:
Tipo 1: Pulverização contra ervas daninhas, Cr$ 500.00 por acre
Tipo 2: Pulverização contra gafanhotos, Cr$ 1000.00 por acre
Tipo 3: Pulverização contra broca, Cr$ 1500.00 por acre
Tipo 4: Pulverização contra tudo acima, Cr$ 2500.00 por acre
Se a área a ser pulverizada é maior do que 1000 acres, o fazendeiro recebe um desconto de 5%. Em adição, qualquer fazendeiro cujo custo ultrapasse Cr$ 750 000.00 recebe um desconto de 10% sobre o valor que ultrapassar Cr$ 750 000.00. Se ambos os descontos se aplicam, aquele relacionado à área é calculado em primeiro lugar. Preparar um algoritmo que leia uma série de cartões contendo as informações:
- Nome do fazendeiro, tipo de pulverização (código de 1 a 4) e a área a ser pulverizada (inteiro)
exemplo:'HILDEBRANDO', 3, 950
Para cada cartão lido, calcular o custo total para o fazendeiro e imprimir o seu nome seguido de sua conta. Utilizar o método fim-de-arquivo para leitura de dados.
sem resoluções.
|
Enunciado 234 Contagem de caracteres |
Strings
Fundamental da Programação em 'C', pág. 92, 1998 Sampaio, I. e Sampaio, A. |
Desenvolva funções para o cálculo das seguintes séries:
Escreva um programa que conte e imprima o número de dígitos, vogais e consoantes lidas do teclado.
sem resoluções.
|
Enunciado 235 Sequência de números |
Números
Trabalho prático, (97/98), 1997 EC, LR, JCN, PP |
Considere a sequência definida como:
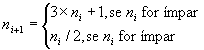
| Resoluções: 1. Sucparip.cat |
|
Enunciado 236 Taxas de juro |
Números
Ciência dos Computadores - Uma abordagem algorítmica, pág. 120, 1983 Tremblay, Bunt |
sem resoluções.
|
Enunciado 237 Valor de uma potência |
Números
Exercícos, 1996 Miguel A. Brito |
Elabore um algoritmo que calcule recursivamente o valor de uma potência (expoente inteiro). Codifique em 'C'
| Resoluções: 1. exprec.c 2. exprec.htm |
|
Enunciado 238 Correspondência sentimental |
Fichas
Ciência dos Computadores - Uma abordagem algorítmica, pág. 121, 1983 Tremblay, Bunt |
Um serviço de correspondência sentimental mantém um arquivo em cartões de seus clientes. Cada cartão contém a seguinte informação:
Preparar uma algoritmo que leia este arquivo e imprima os nomes de
sem resoluções.
|
Enunciado 239 Factorial (recursivo) |
Números
Exercícos, 1996 Miguel A. Brito |
Elabore um algoritmo que calcule recursivamente o factorial de um n.º. Codifique em 'C'.
sem resoluções.
|
Enunciado 240 Fibonacci (Recursivo) |
Números
Exercícos, 1996 Miguel A. Brito |
Elabore um algoritmo recursivo, que calcule o N-ésimo elemento da série de Fibonacci.
| Resoluções: 1. Fibrec.bas |
|
Enunciado 241 Sub-factorial |
Números
Exercícos, 1996 Miguel A. Brito |
Elabore um Algoritmo que calcule recursivamente, o sub-factorial de n:
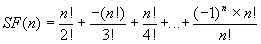
sem resoluções.
|
Enunciado 242 Máquina de trocos |
Números
Exercícos, 1996 Miguel A. Brito |
Elabore um algoritmo que dado um valor determinado valor em escudos, calcule recursivamente quantas moedas de 100$, 50$, 10$, 5$ e 1$, serão necessárias para perfazer essa quantia (com o mínimo de moedas possível). Codifique em 'C'.
sem resoluções.
|
Enunciado 243 Batalha de submarinos |
Jogos
Exercícos, 1996 Miguel A. Brito |
Implementar o jogo da batalha naval mas apenas com submarinos! A dimensão do tabuleiro e o n.º de submarinos em jogo é definido pelo utilizador no início do jogo. Computador e utilizador devem alternar entre si sequências de três tiros, até que um dos dois acerte em todos os submarinos do adversário. Codificar em 'C'.
sem resoluções.
|
Enunciado 244 Batalha de submarinos |
Jogos
Exercícos, 1996 Miguel A. Brito |
Elabore um algoritmo que permita ao utilizador jogar "batalha naval" com o computador, mas apenas com submarinos! O programa deverá escolher aleatoriamente a posição dos seus submarinos tendo o cuidado de não os colocar em casas adjacentes. O primeiro a jogar (utilizador ou computador) deverá ser escolhido aleatoriamente. Computador e utilizador deverão dar como palpites, séries de três tiros, até que um dos dois afunde a esquadra inimiga. Os palpites do computador também deverão ter em conta a impossibilidade dos submarinos serem colocados em casas adjacentes.
sem resoluções.
|
Enunciado 245 Sorteio com bolas |
Jogos
Trabalho prático, (97/98), 1997 EC, LR, JCN, PP |
Na realização de um sorteio é utilizado um sistema composto por bolas numeradas de 0 a 9, colocadas num saco opaco. Para cada lance, são retiradas 3 bolas, uma a uma, sendo cada bola re-colocada no saco depois de mostrada.
Projecte e escreva (na linguagem que é objecto de estudo este semestre) um programa capaz de simular o sorteio acima descrito, tendo em conta o seguinte:
sem resoluções.
|
Enunciado 246 Procura de um valor numa matriz |
Matrizes
Exercícos, 1996 Miguel A. Brito |
Dada uma matriz de inteiros e um valor pedido ao utilizador, procurá-lo na matriz e indicar a primeira posição onde for encontrado. Codificar em 'C'.
| Resoluções: 1. procvm.m 2. procvm.xls |
|
Enunciado 247 Soma de duas matrizes |
Matrizes
Exercícos, 1996 Miguel A. Brito |
Calcular a soma de duas matrizes dadas. Codificar em 'C'.
sem resoluções.
|
Enunciado 248 Resolução de um sistema de equações |
Matrizes
Ciência dos Computadores - Uma abordagem algorítmica, pág. 70, 1983 Tremblay, Bunt |
Um sistema de equações lineares da forma
ax + by = c
dx + ey = f
sem resoluções.
|
Enunciado 249 Transposta de uma matriz |
Matrizes
Exercícos, 1996 Miguel A. Brito |
Calcular a transposta de uma matriz. Codificar em 'C'.
sem resoluções.
|
Enunciado 250 Multiplicação de matrizes |
Matrizes
Exercícos, 1996 Miguel A. Brito |
Calcular a matriz resultante da multiplicação de duas matrizes dadas. Codificar em 'C'.
sem resoluções.
|
Enunciado 251 Multiplicação de matrizes |
Matrizes
Exercícos, 1996 Miguel A. Brito |
Considere uma matriz A de 7 por 5. Desenvolva um algoritmo que:
sem resoluções.
|
Enunciado 252 Rotação de uma matriz |
Matrizes
Exercícos, 1996 Miguel A. Brito |
Rodar uma matriz quadrada de dimensão definida pelo utilizador, 90º para a direita, sem usar matrizes auxiliares ou seja, rodar a matriz através de trocas directa entre os seus elementos. Codificar em 'C'.
sem resoluções.
|
Enunciado 253 Pentadimensional |
Matrizes
Exercícos, 1996 Miguel A. Brito |
Dada uma matriz de inteiros com pentadimensional e um valor pedido ao utilizador, procurá-lo na matriz e indicar a primeira posição onde for encontrado. Codificar em 'C'.
sem resoluções.
|
Enunciado 254 Matriz de temperaturas |
Matrizes
Exercícos, 1996 Miguel A. Brito |
Considere uma matriz que regista as temperaturas obtidas num determinado instante, num determinado espaço tridimensional. Desenvolva um algoritmo que determine quais os pontos interiores em que a temperatura é idêntica à média dos 26 que com ele confinam. Codificar em 'C'.
sem resoluções.
|
Enunciado 255 Matriz de temperaturas |
Matrizes
Exercícos, 1996 Miguel A. Brito |
Considere uma matriz A de 8 por 8. Desenvolva um algoritmo que:
sem resoluções.
|
Enunciado 256 Registo de espectadores |
Matrizes
Exercícos, 1996 Miguel A. Brito |
Considere uma matriz onde são registados os espectadores dos jogos de campeonato de futebol da primeira divisão, dividindo-os em sócios, não sócios, crianças, convidados, imprensa e polícias. Considere um total de 16 estádios e 30 jornadas. Desenvolva um algoritmo que determine e indique:
sem resoluções.
|
Enunciado 257 Naipe |
Jogos
Trabalho prático, (97/98), 1997 EC, LR, JCN, PP |
O "Naipe" é um jogo regido pelas seguintes regras:
sem resoluções.
|
Enunciado 258 Jogo do Galo |
Jogos
Exercícos, 1996 Miguel A. Brito |
Implementar o jogo do galo. O utilizador joga contra o computador. O programa deve ser suficientemente "inteligente" para nunca perder o jogo. Obviamente, deverá detectar automaticamente o fim do jogo (vitória ou empate). Codificar em 'C'.
sem resoluções.
|
Enunciado 259 Número de dias |
Números
Exercícos, s/d Anónimo |
Escreva um programa em Pascal que calcule o número de dias decorridos desde o início do ano até um determinado dia do ano.
sem resoluções.
|
Enunciado 260 soma(n) < limite |
Números
Exercícos, s/d Anónimo |
Escreva um programa que determine qual o maior inteiro n tal que 1+2+3+...+n <= limite, sendo o valor de limite dado pelo Utilizador.
sem resoluções.
|
Enunciado 261 Procurar caracteres em strings |
Strings
Exercícos, 1996 Miguel A. Brito |
Procurar um caracter numa dada string sem recorrer às funções de "string.h". Codificar em 'C'.
sem resoluções.
|
Enunciado 262 Procurar sequência de caracteres em strings |
Strings
Exercícos, 1996 Miguel A. Brito |
Procurar uma sequência de dois caracteres numa dada string sem recorrer às funções de "string.h". Codificar em 'C'.
sem resoluções.
|
Enunciado 263 Ordenar sequência de caracteres em strings |
Strings
Exercícos, 1996 Miguel A. Brito |
Dadas duas strings, ordená-las alfabeticamente sem recorrer às funções de "string.h". Codificar em 'C'.
sem resoluções.
|
Enunciado 264 Eliminação de um elemento de um vector |
Vectores
Fundamental da Programação em 'C', pág. 133, 1998 Sampaio, I. e Sampaio, A. |
Escreva uma função que elimine um elemento de uma dada posição de um vector.
A função deverá retornar o valor do elemento eliminado.
sem resoluções.
|
Enunciado 265 Saudação ao Utilizador |
Strings
Exercícos, 1996 Miguel A. Brito |
Elabore um Algoritmo que pergunte o nome ao utilizador, e responda aleatoriamente com uma de uma série de saudações que tenha em memória (num vector) terminando com o respectivo nome. P. ex.: «"Olá ", nome, "!"», «"Como está ", nome, "?"» ou «"Prazer em vê-lo ", nome, "!"». Arranje uma solução para o facto de a expressão poder ser uma exclamação ou uma questão. Codifique em 'C'.
sem resoluções.
|
Enunciado 266 Numerar os parágrafos de um texto |
Strings
Exercícos, 1996 Miguel A. Brito |
Numerar os parágrafos de um texto (terminado por EOF). Codificar em 'C'.
sem resoluções.
|
Enunciado 267 Procurar sequência de caracteres em strings |
Strings
Exercícos, 1996 Miguel A. Brito |
Procurar uma sequência de caracteres numa linha de texto sem recorrer às funções de "string.h". Codificar em 'C'.
sem resoluções.
|
Enunciado 268 Procurar palavra em linha de texto |
Strings
Exercícos, 1996 Miguel A. Brito |
Procurar uma palavra numa linha de texto sem recorrer às funções de "string.h". Codificar em 'C'.
sem resoluções.
|
Enunciado 269 Eliminar "de", "do" ... |
Strings
Exercícos, 1996 Miguel A. Brito |
Dada uma sequência de nomes de pessoas, eliminar todos os "de" "do" "da" e "e" dos nomes. Codificar em 'C'.
sem resoluções.
|
Enunciado 270 Tratar nomes de pessoas |
Strings
Exercícos, 1996 Miguel A. Brito |
Dada uma sequência de nomes de pessoas, converter todas as palavras em minúsculas, e em maiúsculas todas as primeiras letras de cada palavra. Codificar em 'C'.
sem resoluções.
|
Enunciado 271 Conversão entre bases |
Strings
Exercícos, 1996 Miguel A. Brito |
Converter um n.º numa dada base de numeração à escolha do utilizador, convertê-lo para qualquer outra base também à escolha do utilizador. Codificar em 'C'. sem resoluções.
| Resoluções: 1. convbass.htm 2. convbass.m 3. convbas.xls |
|
Enunciado 272 Leitura de um texto |
Strings
Exercícos, 1996 Miguel A. Brito |
Ler um texto até EOF. No final indicar o n.º de letras, de palavras e de linhas desse texto. Codificar em 'C'.
sem resoluções.
|
Enunciado 273 Leitura de um texto e inversão das palavras |
Strings
Exercícos, 1996 Miguel A. Brito |
Dado um texto (ler até EOF) apresentá-lo com as letras de cada palavra escritas de trás para a frente (p. ex.: "de tras para a frente" => "ed sart arap a etnerf"). Codificar em 'C'.
sem resoluções.
|
Enunciado 274 Ordenação de nomes de pessoas |
Strings
Exercícos, 1996 Miguel A. Brito |
Dada uma sequência de nomes de pessoas, apresentá-los ordenados por ordem alfabética. Codificar em 'C'.
sem resoluções.
|
Enunciado 275 Substituição de 8 espaços por tabs |
Strings
Exercícos, 1996 Miguel A. Brito |
Considerando que um tab corresponde a tabulações de oito caracteres, substituir todos os espaços que for possível por tabs. Codificar em 'C'.
sem resoluções.
|
Enunciado 276 Conversão de formatos de datas |
Strings
Exercícos, 1996 Miguel A. Brito |
Converter uma data no formato "dd-mm-aaaa" no formato "dd de mês de aaaa". P. ex.: "01-03-1998" => "01 de Março de 1998". Codificar em 'C'.
sem resoluções.
|
Enunciado 277 Número por extenso |
Strings
Exercícos, 1996 Miguel A. Brito |
Converter um valor numérico no seu extenso. P. ex.: 1 234 => "mil duzentos e trinta e quatro". Codificar em 'C'.
sem resoluções.
|
Enunciado 278 Procura |
Vectores
Exercícos, 1996 Miguel A. Brito |
Dado um vector em que cada elemento é uma estrutura composta por número e nome de um aluno, elaborar um algoritmo que dado o número, indique o respectivo nome. Codificar em 'C'.
sem resoluções.
|
Enunciado 279 Troca |
Vectores
Exercícos, 1997 Matos, A. |
Escreva uma parte de um programa que troque simetricamente os n elementos de um vector, isto é, o primeiro elemento troca com o último, o segundo com o penúltimo, etc.
Por exemplo; se o vector inicial for [8 5 6 1 3], a sua situação final deverá ser: [3 1 6 5 8]
sem resoluções.
|
Enunciado 280 Inserção |
Vectores
Exercícos, 1997 Matos, A. |
Escreva uma função que insira um elemento x na posição i de um array com n elementos, deslocando previamente os elementos a[i], ..., a[n-1] para a direita. Por exemplo, se o array original for: [8 5 6 1 3], e x=12 e i=3, deve resultar [8 5 6 12 1 3]
sem resoluções.
|
Enunciado 281 Intersecção |
Vectores
Exercícos, 1997 Matos, A. |
São dados dois arrays, a[] e b[] com, respectivamente, m e n elementos. Pretende-se imprimir os elementos que pertencem à intercepção dos conjuntos representados pelos dois arrays. Por exemplo, se os arrays são [8 6 5 1 3] e [2 1 4 6], devem ser impressos os valores 6 e 1.
sem resoluções.
|
Enunciado 282 Três vectores |
Vectores
Exercícos, 1996 Miguel A. Brito |
Ler três vectores, respectivamente com a informação referente ao número, nome e nota dos alunos de uma turma. Depois de carregados os três vectores, copiar toda a informação para um único vector em que cada registo é compostos por uma estrutura com os campos número, nome e nota. Codificar em 'C'.
sem resoluções.
|
Enunciado 283 Área e diagonal |
Geometria
Exercícos, 1996 Miguel A. Brito |
Calcular a área e o comprimento da diagonal de um rectângulo dado. O rectângulo deve ser definido através de uma estrutura composta por dois pontos. Por sua vez, cada ponto é definido através de uma estrutura composta por duas coordenadas x e y. Codificar em 'C'.
sem resoluções.
|
Enunciado 284 Inserção ordenada num vector de estruturas |
Vectores
Exercícos, 1996 Miguel A. Brito |
Fazer um algoritmo para a inserção ordenada (por número) de um vector de estruturas do tipo {número, nome, nota} para armazenar as notas finais dos alunos da disciplina de programação de computadores. A procura do local de inserção deve ser feita através de uma pesquisa binária (divisão sucessiva do vector a meio).
sem resoluções.
|
Enunciado 285 Lista de telefones |
Vectores
A Chave para o Mundo dos Computadores, Publipress Editora, 1984 Lohberg, Lutz |
Construa um programa que permita gerir uma lista telefónica com os items nome e número de telefone. O acesso às várias funções deverá ser obtido através de um menu com as seguintes opções:
sem resoluções.
|
Enunciado 286 Inserção ordenada num vector de estruturas |
Matrizes
Exercícos, 1996 Miguel A. Brito |
Aceitar reservas para uma sala de espectáculos, atribuindo automaticamente os respectivos lugares (dispostos numa matriz de F Filas por C Cadeiras). O cliente pode pedir lugares para a parte da frente ou de trás da sala. No fim imprimir um mapa da ocupação da sala e uma lista das reservas, ordenada pelo último nome do cliente, e com a indicação se está pago ou não. Refine o algoritmo de modo a aceitar desistências e a evitar que os lugares de uma reserva fiquem separados (seja intercalados com outros, seja em filas diferentes). Codificar em 'C'.
sem resoluções.
|
Enunciado 287 Inserção ordenada num vector de estruturas |
Vectores
Exercícos, 1996 Miguel A. Brito |
Fazer um algoritmo que deduza um resultado através de sucessivas perguntas de resposta tipo Sim/Não a que o utilizador vai respondendo.
No fim, se não acertar, deve pedir ao utilizador a resposta correcta e a pergunta que deveria ter feito para conseguir distinguir entre a resposta que deu e a que deveria ter dado.
Na vez seguinte, o programa já "aprendeu" a dar mais uma resposta correcta!
O programa pode saber se está a fazer uma pergunta ou se já está a dar a resposta pelo valor dos apontadores (p. ex. se forem 0 - já não há mais perguntas - é a resposta).
Exemplo para adivinhar o nome de um elemento da turma: "É do sexo masculino?" - sim - "É loiro?" - não - "É o Paulo?" - não - "Então quem era?" - Nuno - "Indique uma característica que o distinga do Paulo" - É alto - ; Na próxima vez, se não for loiro, o computador em vez de sugerir "Paulo" deve perguntar se é alto: se for, é o Nuno se não é o Paulo.
sem resoluções.
|
Enunciado 288 Quadrado mágico |
Matrizes
Exercícos, 1996 Miguel A. Brito |
Calcular (por tentativas) a distribuição dos números de 1 a 9 numa matriz 3x3, de modo que a soma dos elementos de qualquer linha qualquer coluna e qualquer diagonal seja sempre 15.
| Resoluções: 1. quadm2.mws 2. quadm2.m |
|
Enunciado 289 Operações sobre matrizes |
Matrizes
Fundamental da Programação em 'C', pág. 133, 1998 Sampaio, I. e Sampaio, A. |
Operações sobre matrizes
sem resoluções.
|
Enunciado 290 Conversão de inteiros e strings |
Vectores
Fundamental da Programação em 'C', pág. 133, 1998 Sampaio, I. e Sampaio, A. |
Conversão de inteiros e strings
sem resoluções.
|
Enunciado 291 Procura em strings |
Vectores
Fundamental da Programação em 'C', pág. 134, 1998 Sampaio, I. e Sampaio, A. |
Desenvolva uma função que devolva o índice da primeira ocorrência de um dado caracter numa string. O cabeçalho da função deverá ser:
sem resoluções.
|
Enunciado 292 Procura em strings |
Vectores
Fundamental da Programação em 'C', pág. 134, 1998 Sampaio, I. e Sampaio, A. |
Desenvolva uma função que dadas duas strings retorne o índice da 1ª ocorrência na 1ª string de qualquer caracter da 2ª, ou -1 se não encontrar.
sem resoluções.
|
Enunciado 293 Procura em strings |
Vectores
Fundamental da Programação em 'C', pág. 134, 1998 Sampaio, I. e Sampaio, A. |
Escreva uma função que dadas duas strings pesquise a existência da segunda na primeira e, caso a encontre, retorne o índice da posição onde a 2ª se inicia na primeira. Se não encontrar, a função deverá retornar -1. A posição a partir da qual se inicia a pesquisa também deverá ser dada como argumento. Não usar a função padrão strstr.
sem resoluções.
|
Enunciado 294 Tuplos |
Vectores
, 2001 Miguel Brito, Pedro Pimenta |
Elabore e codifique em 'C', um algoritmo que permita ao utilizador introduzir as seguintes características de um conjunto de automóveis: marca, cor e kilometragem. Esses dados deverão ser armazenadas num vector de tuplos.
O programa deverá terminar a introdução de dados quando a cor introduzida for "transparente".
Escreva uma função, a invocar após a introdução dos dados, que receba como argumento um vector de tuplos (com a estrutura adequada) e devolva:
sem resoluções.
|
Enunciado 295 Tuplos |
Vectores
, 2001 Miguel Brito, Pedro Pimenta |
Elabore e codifique em 'C', um algoritmo que permita ao utilizador introduzir as seguintes características de um livro: Autor, ano de edição, nº de páginas. Esses dados deverão ser armazenadas num vector de tuplos.
O programa deverá terminar a introdução de dados quando o Utilizador introduzir o autor "XPTO".
Escreva uma função, a invocar após a introdução dos dados, que receba como argumento um vector de tuplos (com a estrutura adequada) e devolva:
sem resoluções.
|
Enunciado 296 Tuplos |
Vectores
, 2001 Miguel Brito, Pedro Pimenta |
Elabore e codifique em 'C', um algoritmo que permita ao utilizador introduzir as seguintes características de um conjunto de automóveis: marca, cor e kilometragem. Esses dados deverão ser armazenadas num vector de tuplos.
O programa deverá terminar a introdução de dados quando a cor introduzida for "nenhuma".
Escreva uma função, a invocar após a introdução dos dados, que receba como argumento um vector de tuplos (com a estrutura adequada) e imprima no ecran:
sem resoluções.
|
Enunciado 297 Tuplos |
Vectores
, 2001 Miguel Brito, Pedro Pimenta |
Elabore e codifique em 'C', um algoritmo que permita ao utilizador introduzir as seguintes características de um jogador de futebol: nome, idade, equipa actual. Esses dados deverão ser armazenadas num vector de tuplos.
O programa deverá terminar a introdução de dados quando o Utilizador introduzir o jogador "XPTO".
Escreva uma função, a invocar após a introdução dos dados, que receba como argumento um vector de tuplos (com a estrutura adequada) e imprima no ecran:
sem resoluções.
|
Enunciado 298 Tuplos |
Vectores
, 2001 Miguel Brito, Pedro Pimenta |
Elabore e codifique em 'C', um algoritmo que permita ao utilizador introduzir as seguintes características de um jogador de futebol: nome, idade, equipa actual. Esses dados deverão ser armazenadas num vector de tuplos.
O programa deverá terminar a introdução de dados quando o Utilizador introduzir o jogador de nome "XPTO".
Escreva uma função, a invocar após a introdução dos dados, que receba como argumento um vector de tuplos (com a estrutura adequada) e imprima no ecran:
- Quantos jogadores foram registados com nome iniciado por 'G' ou 'T';
- Quais os jogadores com mais de 23 anos e que pertençam a uma equipa com o nome começado por 'B';
sem resoluções.
|
Enunciado 299 Mastermind |
Jogos
, 2001 Miguel Brito |
Elabore um Algoritmo que permita ao utilizador jogar “Master Mind”; o programa deve gerar aleatoriamente a combinação a descobrir, e depois responder a cada palpite do utilizador, indicando o n.º de elementos certos na casa certa, e o n.º de elementos certos na casa errada.
O número de elementos e de cores a usar, deve ser pedido ao utilizador no início do programa (os valores típicos são 4 e 6 respectivamente). O jogador deve ter a possibilidade de desistir! Quando o utilizador acertar na combinação gerada, o programa deve indicar o n.º de jogadas em que o fez. Codifique em 'C'.
sem resoluções.
|
Enunciado 300 Folhas arrancadas |
Números
, Público, 2001 José Paulo Viana |
A Alexandra comprou um caderno de 100 folhas com as páginas numeradas de 1 a 200. O irmão mais novo encontrou o caderno e arrancou-lhe 21 folhas. A Alexandra encontrou as folhas arrancadas e resolveu somar os 42 números que lá estavam. No fim, comunicou ao Afonso:
- Olha a coincidência. A soma destes 42 números é precisamente o ano em que estamos: 2001.
Mas o Afonso respondeu-lhe logo:
- De certeza que te enganaste.
Quem tem razão ?
[Este enunciado pode ser modificado para ter várias soluções, e sugerido definir e implementar um algoritmo que as determine. PCP, Dez. 02]
sem resoluções.
|
Enunciado 301 Jogo da Glória |
Jogos
, s/d anónimo |
O jogo será jogado entre dois jogadores. O tabuleiro do jogo é constituído por 60 casas, numeradas de 1 a 60. Em cada jogada o jogador lança dois dados, e avança um número de casas igual ao valor apresentado pelos dados. Algumas casas do tabuleiro do jogo são especiais, e têm os seguintes ssignificados:
| Casa | Acção |
| 8 | fica uma vez sem jogar |
| 12 | avança para a casa 30 |
| 15 | voltar ao início |
| 20 | fica uma vez sem jogar |
| 34 | avança para a casa 42 |
| 37 | voltar ao início |
| 40 | fica uma vez sem jogar |
| 45 | avança para a casa 52 |
| 48 | voltar ao início |
| 50 | fica uma vez sem jogar |
sem resoluções.
|
Enunciado 302 Inversão de uma string |
Strings
, 1999 Virgílio Vilela |
Elaborar um programa que lê uma cadeia de caracteres e mostra-a invertida na tela. Após, o programa volta para ler outra, assim fazendo até que a cadeia nula seja nula, isto é, sem nenhum caractere.
sem resoluções.
|
Enunciado 303 Eliminação de um caractere |
Strings
, 1999 Virgílio Vilela |
Fazer um programa que lê uma cadeia e um caractere e elimina todas as ocorrências do caractere na cadeia. Após, o programa pede nova cadeia e só termina quando a cadeia lida for nula.
sem resoluções.
|
Enunciado 304 Quantidade de caracteres |
Strings
, 1999 Vírgilio Vilela |
Elaborar um programa que lê uma cadeia e um caractere e informa a quantidade de ocorrências do caractere na cadeia (não diferenciar minúsculas/maiúsculas: 'a' = 'A'). Por exemplo, se a cadeia for "BANANA nanica" e o caractere for "a", o programa deve informar 5.
sem resoluções.
|
Enunciado 305 Estatística de frase |
Strings
, 1999 Vírgilio Vilela |
Elabore um programa que lê uma cadeia de até 255 caracteres e informa:
- quantidade de brancos
- quantidade de palavras
- quantidade de ocorrências da letra 'A'
sem resoluções.
|
Enunciado 306 Estatística de frase |
Strings
, 1999 Vírgilio Vilela |
Altere o programa acima(anterior) para que informe também a quantidade de cada vogal.
sem resoluções.
|
Enunciado 307 Validação de senha |
Strings
, 1999 Vírgilio Vilela |
Escrever um programa que lê uma senha (entre 4 e 8 caracteres), compara a senha linha com o valor correto e informa se o usuário está autorizado ou se a senha está incorreta. A senha correta é registrada dentro do programa como uma constante. O programa permite até 3 tentativas.
sem resoluções.
|
Enunciado 308 Trajectória de projéctil |
Números
, 2000 Dias, M., Martins, F. |
Uma das primeiras aplicações dos computadores foi o cálculo de trajectórias de projécteis. Se um projéctil é atirado com uma velocidade
inicial de v (m/s), segundo um ângulo com a horizontal de q (graus), a sua posição (x, y) no plano vertical, em cada instante t (segundos) pode ser calculada, desprezando a resistência do ar, pelas seguintes expressões:
x = (v cosq)t e
y = (v sinq)t - 0.5gt2onde 0 <= q <= p/ 2 e g = 9.8 m/s2.
Desenvolva uma folha Excel para listar as coordenadas x e y para um tiro correspondente a valores de v e q fornecidos pelo utilizador. A listagem
deve ser feita para um número dado de intervalos, nint e terminar quando o projéctil atinge o solo , isto é t = t f e y=0. O valor de t f e as coordenadas
x e y devem ser determinadas por funções VBA.
sem resoluções.
|
Enunciado 309 Partição de um conjunto |
Números
, 2003 Pimenta, P. |
Crie um programa que inicialize um conjunto de 30 números com valores aleatórios entre 0 e 20.
Procure depois criar partições do conjunto anterior para as quais:
- A soma dos valores em cada uma das partições seja igual;
- A soma dos quadrados dos valores em cada uma das partições seja igual;
- A soma dos cubos dos valores em cada uma das partições seja igual;
- ...
sem resoluções.
|
Enunciado 310 Clientes de um banco |
Fichas
Ciência dos Computadores - Uma abordagem algorítmica, pág. 122, 1983 Tremblay, Bunt |
Mais e mais bancos estão passando para sistemas mecanizados de contas de clientes. Desenvolver um algoritmo para processar as transacções num sistema hipotético. Considerar que as contas dos clientes são mantidas num conjunto de cartões (em ordem crescente de número de conta), cada uma com o seguinte formato:
| nome do cliente | número de conta | saldo actual | |
| Exemplo: | 'ANTONIO BAKOWSKI' | 501865 | 298 337.82 |
| nome do cliente | número de conta | acção | valor | |
| Exemplo: | 'MOACIR R. A. PRADO' | 308512 | 'DEPOSITO' | 162 327.30 |
Os cartões de transacções são processados da seguinte forma: um 'DEPOSITO' leva a adicionar um valor ao saldo do cliente; uma 'RETIRADA' leva a subtrair um valor do saldo do cliente; uma 'CONTA NOVA' leva à criação de um novo registro com um valor dado como saldo em aberto. À medida que cada cartão de transacção é processado, uma linha é impressa, dando o formato do novo cartão para este cliente. Estes cartões serão perfurados e inseridos manualmente no conjunto de cartões a serem processados de novo mais tarde.
Note que a inclusão de ambos, nome do cliente e número de conta no cartão de transacções, serve como uma segurança no processo de atualização. Embora a informação seja processada pelo número da conta, se o nome no cartão de transação não confere com o do arquivo do cliente, a transação é ignorada e uma mensagem apropriada é emitida.
Preparar um algoritmo que leia os dois conjuntos de cartões simultaneamente a partir de diferentes leitoras de cartões (utilizar Leia1 para a primeira leitora e Leia2 para a segunda). Em seguida, processar os cartões de transacções contra o arquivo do cliente, como descrito, e produzir a saída apropriada (informação atualizada e mensagens de erro). Utilizar o método fim-de-arquivo para indicar o fim dos cartões de entrada das duas leitoras.
sem resoluções.
|
Enunciado 311 Maior e menor |
Vectores
Ciência dos Computadores - Uma abordagem algorítmica, pág. 132, 1983 Tremblay, Bunt |
Para um vetor A de n números reais, formular um algoritmo que determine o maior e o segundo maior elemento deste vetor. Assumir que estes valores são distintos.
sem resoluções.
|
Enunciado 312 Maior diferença entre elementos consecutivos |
Vectores
Ciência dos Computadores - Uma abordagem algorítmica, pág. 132, 1983 Tremblay, Bunt |
Para um vetor A de n números reais, obter a maior diferença entre dois elementos consecutivos deste vetor.
sem resoluções.
|
Enunciado 313 Menor diferença entre elementos consecutivos |
Vectores
Ciência dos Computadores - Uma abordagem algorítmica, pág. 133, 1983 Tremblay, Bunt |
Repetir o exercício anterior e obter a menor diferença entre dois elementos consecutivos.
sem resoluções.
|
Enunciado 314 Estatísticas |
Vectores
Ciência dos Computadores - Uma abordagem algorítmica, pág. 133, 1983 Tremblay, Bunt |
Formular um algoritmo para obter as seguintes estatísticas para um vetor X de n elementos:
Desvio médio (DM) = 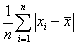 onde
onde 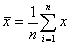
Raiz quadrática média (RMQ) = 
Média harmónica (MH) = 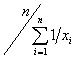
Amplitude total (AT) = máx {x1, x2, ..., xn} - min{x1, x2, ...xn}
Média geométrica (MG) = 
sem resoluções.
|
Enunciado 315 Sucessões |
Números
Manual da TI 83, pág. 177, 2000 |
Uma pequena floresta com 4000 árvores está ao abrigo de um novo plano de florestação, que prevê que sejam abatidas, anualmente, 20% das árvores, e que sejam plantadas 1000 novas árvores. Será que a floresta vai desaparecer? O processo estabilizará o tamanho da floresta? Se assim for, daqui a quantos anos e com quantas árvores ?
sem resoluções.
|
Enunciado 316 Omissão de valores repetidos |
Números
Ciência dos Computadores - Uma abordagem algorítmica, pág. 133, 1983 Tremblay, Bunt |
Preparar um algoritmo que leia um vetor A não ordenado de n inteiros e imprima o vetor na mesma sequência, ignorando os valores em duplicata encontrados no vetor lido. O número de elementos restantes (m) é também solicitado. Por exemplo, dado o vetor
| A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| 15 | 31 | 23 | 15 | 75 | 23 | 41 | 15 | 31 | 85 |
de 10 inteiros, o vetor resultante seria
| A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| 15 | 31 | 23 | 75 | 41 | 85 |
com m=6
sem resoluções.
|
Enunciado 317 Cálculo Matricial |
Matrizes
Luís Lima, 1986 |
Pretende-se, dada uma matriz quadrada A, calcular AAT. Atendendo ao facto de que AAT é uma
matriz simétrica, e sem calcular explicitamente a transposta AT matriz, escreva:
- Um algoritmo para ler a matriz, efectuar a operação descrita e escrever o resultado
- Um programa BASIC que implemente o algoritmo
sem resoluções.
|
Enunciado 318 Distribuição |
Pedro Pimenta, 2007 |
Faça um programa que simule dez lançamentos de um dado, e analise a frequência de cada resultado possível. Repita o processo para 100, 200, 300, 400, ..., 1000 e 2000 lançamentos, e compare a distribuição obtida com o cálculo das respectivas probabilidades. Compare os resultados obtidos (e o tempo de cálculo) com várias ferramentas de cálculo / linguagens de programação.
| Resoluções: 1. ex318.bas 2. ex318.xls |
|
Enunciado 319 Distribuição |
Pedro Pimenta, 2007 |
Faça um programa que simule dez lançamentos de dois dados, e analise a frequência de cada resultado possível. Repita o processo para 100, 200, 300, 400, ..., 1000 e 2000 lançamentos, e compare a distribuição obtida com o cálculo das respectivas probabilidades. Compare os resultados obtidos (e o tempo de cálculo) com várias ferramentas de cálculo / linguagens de programação.
sem resoluções.
|
Enunciado 320 Distribuição |
Pedro Pimenta, 2007 |
Faça um programa que simule dez lançamentos de um três dados, e analise a frequência de cada resultado possível. Repita o processo para 100, 200, 300, 400, ..., 1000 e 2000 lançamentos, e compare a distribuição obtida com o cálculo das respectivas probabilidades.
Compare os resultados obtidos (e o tempo de cálculo) com várias ferramentas de cálculo / linguagens de programação.
sem resoluções.
|
Enunciado 321 Distribuição |
Pedro Pimenta, 2007 |
Faça um programa que simule 100 lançamentos de um moeda, e analise a frequência de cada resultado possível. Determine, também qual o "comprimento" da maior sequência de caras e da maior sequência de coroas, e determine a frequência de todas as sequências encontradas.
Repita o processo para 200, 300, 400, ..., 1000 e 2000 lançamentos, e compare a distribuição obtida com o cálculo das respectivas probabilidades.
Compare os resultados obtidos (e o tempo de cálculo) com várias ferramentas de cálculo / linguagens de programação.
sem resoluções.
|
Enunciado 322 Análise |
Strings
Pedro Pimenta, 2007 |
Considere um sistema ortonormado, plano, referenciável pelas direcções N (Norte), S (Sul), E (Este) e O (Oeste).
Considere uma cadeia de caracteres do tipo:
como descritora de uma posição inicial (50, 80) e de movimentos unitários em cada uma das direcções indicadas.
Faça um programa que ´interprete´ uma cadeia de caracteres do tipo indicado, e que calcule:
1. a posição final do móvel
2. a distância entre as posições inicial e final
3. o número de movimentos mínimo (e quais) que permite a mesma deslocação
sem resoluções.
|
Enunciado 323 Análise |
Strings
Pedro Pimenta, 2007 |
Considere um sistema ortonormado, plano, referenciável pelas direcções N (Norte), S (Sul), E (Este) e O (Oeste).
Considere uma cadeia de caracteres do tipo:
como descritora de uma posição inicial (50, 80) e de movimentos unitários em cada uma das direcções indicadas. Faça um programa que:
1. Gere uma posição inicial e uma trajectória aleatória (Considere a sugestão de usar um dodecaedro - poliedro regular de 12 faces - como ´dado´ para obter as direcções de movimentação; 1, 2 ou 3 - N; 4, 5 ou 6 - O; 7, 8 ou 9 - S, 10, 11 ou 12 - E), e que ´interprete´ a cadeia de caracteres gerada, calculando:
2. a posição final do móvel
3. a distância entre as posições inicial e final
e
4. o número de movimentos mínimo (e quais) que permite a mesma deslocação
Repita os passos anterioeres considerando dois (ou mais) móveis, e calcule:
5. A evolução da distância entre os móveis 6. A ocurrência de colisões
sem resoluções.
|
Enunciado 324 Áreas |
Pedro Pimenta, 2007 |
Considere a parábola (y=-x2 + 6x - 5) representada na seguinte figura:
- a área assinalada por "A"
- a área assinalada por "B"
sem resoluções.
|
Enunciado 325 Análise estatística |
Pedro Pimenta, 2007 |
Considere o alvo representado na figura seguinte:
x = 50 + 60*(R-0,5)
y = 50 + 60*(R-0,5)
sendo R um valor aleatório de domínio ]0, 1[.
O programa deverá, para cada corrida de N lançamentos, determinar as seguintes características da distribuição dos pontos obtidos:
- a média
- a moda
- a variância
- o desvio padrão
- a curtose
- obter os parâmetros anteriores para um número diferente de dardos
- Obter os parâmetros anteriores para outras funções geradoras do par (x, y), como:
- x = 50 + 60*(R-0,5)
y = 50 + 60*(R-0,5)
- x = 50 + 30*(R-0,5) + 30*(R-0,5)
y = 50 + 30*(R-0,5) + 30*(R-0,5)
- x = 50 + 60*(R-0,5)
sem resoluções.
|
Enunciado 326 Análise estatística |
Pedro Pimenta, 2007 |
No jogo de tiro ao alvo que lhe propõem, deverá lançar dardos em direcção ao alvo representado na figura seguinte:

- x = 55 + A*(R-0,5) + C*(R-0,5)2
y = 45 + B*(R-0,5) + D*(R-0,5)3
ii) Considere agora que poderá alterar os parâmetros (iniciais) de tiro:
, de acordo com as seguintes regras:
- pode investir 120 Euros na alteração dos parâmetros de tiro (A, B, C e D).
- A alteração de 10% do valor de cada um dos parâmetros custa 30 euros
sem resoluções.
|
Enunciado 327 Quadros de letras |
Pedro Pimenta, 2007 |
Conhece, concerteza, o passatempo de procurar palavras num quadro de letras, como o representado a seguir:
J U G C C G E T X B I N L E M O Y K N S
C C E U X V A F C Q F N Q J C U H O O O
R W Q W P Y E Z R E D B H C C J H N N B
P M D G C L G U Z R Q F I W A N Q K F R
A K M N I Z J W G D N U W A Y W G R U U
R M N N S V A P P Q G C F G U B K A K M
Z Z W W H L X A M S D X A B Z C X S X N
P E T P U O E F B J T L J C N O G C L T
Q B K F R X Y W A Y Q O H M W Y D O K L
V Z G L R O V Q W Y V Z G K E Q S X J R
Y T K L X Q C U M B L Z C G O W O V U M
L H Z I D S O F U P M U O X F Q F G S W
P O I I R P O I J O B E J G Y W H V V H
L U M C S P L U Q S D L V B Z V A D X X
K E E A U P Y P X T C F F J L U P V Y U
F G Y I X J F E G K I Z A R W T L F P T
K V U U R B B G R Q P I L C Q A Q I K E
Z K V G G W D M R G L X N X C D L M F Z
X N J J N E J M E B U B V Y I J S Q K Y
Deverá criar um programa que, dada uma matriz como a representada acima, e uma lista de palavras (p. ex.: elefante, leão, rinoceronte, papagaio, etc..) procure as palavras na matriz segundo as direcções de leitura normal: horizontal, da esquerda para a direita, e vertical, de cima para baixo.
Modifique o programa anterior para procure palavras escritas em várias direcções:
Modifique o seu programa para determinar o tempo de procura, e relacione o tempo de procura com a dimensão da matriz e o tamanho da lista de palavras a procurar.
sem resoluções.